1 / 4

Solving Triangle Distances Between Fire Towers A and B

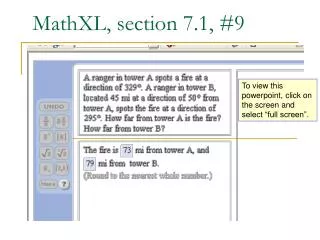
This exercise illustrates how to find angles A, B, and F in a triangle formed by two fire towers and a fire site. Tower A is located at a bearing of 329°, and Tower B at 295°, with various angles provided (angle A = 50°, angle B = 65.45°, angle F = 81°). Using these angles, we calculate the distances from the fire to each tower: 73 miles from Tower A and 79 miles from Tower B. The problem emphasizes application of trigonometric principles in navigation and distance measurement.

aaron-robinson
Télécharger la présentation

Solving Triangle Distances Between Fire Towers A and B

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. MathXL, section 7.1, #9 To view this powerpoint, click on the screen and select “full screen”.

  2. Draw the picture Fire Tower B 295o 45 miles 50o Tower A 329o

  3. Find angle A, angle Band angle F. F B 65o 45 81o A Angle A 50o 329o 295o Angle B 50o Angle A = 360 – 329 + 50 Angle B = 295 – 180 – 50

  4. Solve the triangle. F F = 180 – 81 – 65 34o BF = 79 miles B 65o 45 81o AF = 73 miles A The distance from tower A to the fire is 73 miles and from tower B to the fire is 79 miles.

More Related