Line Segment Intersection

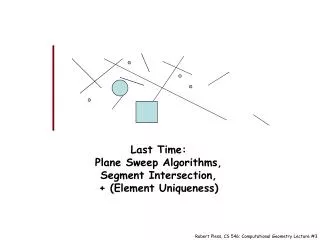
1. Line Segment Intersection • Chapter 2 of the Textbook • Driving Applications • Map overlap problems • 3D Polyhedral Morphing M. C. Lin

2. Thematic Map Overlay • GIS systems split each map into several layers • Each layer is called a thematic map, storing one type of information • Find overlay of several maps to locate interesting junctions M. C. Lin

3. Transform to a Geometric Problem • Curves can be approximated by small (line) segments • Each thematic map can be viewed as a collection of line segments • Finding the overlay of two networks => computing all intersection points between the line segments of two sets M. C. Lin

4. Let’s Be More Serious & Precise... • Segments closed or open? • Take a look at the original problem => should be closed • To simplify further, make 2 sets into 1 • But, how do we identify the really interesting one? Filter them out by checking if they are from the same set. M. C. Lin

5. y x Problem Analysis • Brute Force Approach: O(n2) • Desiderata: output(intersection) sensitive • Segments that are close together are the candidates for intersection M. C. Lin

6. event point l : sweep line Plane Sweep Algorithm • Status of l: the set of segments intersecting l • Event points: where updates are required M. C. Lin

7. Plane Sweep Algorithm (cont) • At a event point: update the status of the sweep line & perform intersection tests Upper: a new segment is added to the status of l and it’s tested against the rest Lower: it’s deleted from the status ofl => Only testing pairs of segments for which there is a horizontal line intersects both segments. => But, this is not good enough. It may still be inefficient, O(n2) for some cases. (ex) a set of segments all intersect with x-axis. M. C. Lin

8. l Sm Sk Sj Sl Plane Sweep Algorithm (cont) To include the idea of being close in the horizontal direction, only test segments that are adjacent in the horizontal direction -- • Only test each with ones to its left and right • New “status”: ordered sequence of segments • New “event points”: endpoints and intersects M. C. Lin

9. Nasty Cases (Degeneracies) • Horizontal lines • Overlapping line segments • Multiple line segments intersect at one single point M. C. Lin

10. Plane-Sweep Algorithm (Recap) • Move a horizontal sweep line l downwards • Halt lat event points (end pts & intersects) • While l moves, maintain ordered sequence of segments intersected by it • When l halts at an event point, the sequence of segments changes, status of l needs to be updated and to detect intersections depending on type of events M. C. Lin

11. Event Types NOTE: only intersection points below l are important, assuming all intersection points above l have been computed correctly. • Upper end point: If Siand Sk are adjacent on l, a new upper end point of Sjappears, check Sjwith Si and Sk for intersections • Intersection point of 2 lines: Change their order. Each gets (at most) 1 new neighbor • Lower end point: Its two neighbors are now adjacent and must be tested for intersection below the sweep line l M. C. Lin

12. Data Structure • Type: Event queue that stores events • Operations • remove next event and return it to be treated • among 2 events with the same y-coordinate, the one with smaller x-coordinate is returned (left-to-right priority order) • allow for insertions & check if it is already there • allow 2++ event points to coincide (ex) two upper end points coincide M. C. Lin

13. Implementing Event Queue • Define an order on event points, according to which they will be handled • Store the event points in a balanced binary search tree T according to their orders • both fetching & insertion takes O(log m) time, where m is the number of events • Maintain the status of l using T • the left-to-right order of segments on the line l <=> the left-to-right order of leaves in T • segments in internal nodes guide search • each update and search takes O(log m) M. C. Lin

14. l Sm Sl Sk Si Sj Sk Sl Si Sj Sm Sl Si Sk Sj Status Structure, T T M. C. Lin

15. FindIntersections (S) • Input : a set S of line segments in a plane • Output : a set of intersections and their associated line segments in S 1. Initialize Q. Insert the end points into Q with their corresponding segments 2. Initialize an empty status structure T 3. While Q is not empty 4. Do Find next event point p in Q & delete it 5. HandleEventPoint (p) M. C. Lin

16. S1 S3 S4 S8 S7 S5 l S1 S3 S2 Handling Changes in Status M. C. Lin

17. T T S1 S2 S5 S3 S3 S1 S4 S7 S8 S7 S3 S8 S1 S2 S1 S3 S7 S4 S1 S4 S7 S5 S3 S8 S7 S5 l S1 S3 Handling Changes in Status S2 M. C. Lin

18. HandleEventPoint (p) 1. Let U(p) be set of segments whose upper end point is p 2. Search in T for set S(p) of all segments that contains p; they are adjacent in T. Let L(p)  S(p) be the set of segments whose lower endpts in p and C(p)  S(p) be the set of segments that contains p in its interior 3. If L(p)  U(p)  C(p) contains more than 1 segment 4. then Report p as an intersect with L(p), U(p) and C(p) 5. Delete segments in L(p)  C(p) from T 6. Insert segments in U(p)  C(p) into T. Order segments in T according to their order on sweep line just below p. A horizontal one comes last among all containing p. M. C. Lin

19. HandleEventPoint (p) 7. (Deleting & re-inserting segments of C(p)reverses order) 8. If U(p)  C(p) = 0 9. then Let sl and sr be the left/right neighbors of p in T 10. FindNewEvent(sl , sr , p) 11. else Let s’be the left most segment of U(p)  C(p) in T 12. Let sl be the left neighbor of s’in T 13. FindNewEvent(sl , s’, p) 14. Find s’’be rightmost segment of U(p)  C(p) in T 15. Let sr be the right neighbor of s’’ in T 16. FindNewEvent(s’’, sr, p) M. C. Lin

20. FindNewEvent (sl, sr, p) 1. If sl and sr intersect below the sweep line, or on it and to the right of current point p, and the intersection is not yet present as an event in Q 2. Then Insert the intersection point as an event into Q M. C. Lin

21. Algorithm Analysis • Let S be a set of n segments in a plane • All intersections in S can be reported in • O(n log n + I log n) time • O(n) space • where I is the number of intersection points M. C. Lin

22. Doubly-Connected Edge List • 3 records: vertices, faces and “half-edges” • Vertex: coordinates(v) & a ptr to a half-edge • Face: • OuterComponent(f): bounding edges • InnerComponent(f): edges on the boundary of holes contained in the face, f • Edge: a ptr to Origin(e), a ptr to a twin-edge, ptrs to Next(e) & Prev(e) edges and its left IncidentFace(e) M. C. Lin

23. Computing Overlay of Subdivisions • Let S1, S2 be two planar subdivisions of complexity n1 and n2 respectively; and let n = n1 + n2 • Overlay of S1 and S2can be constructed in O(n log n + k log n) time, where k is the complexity of overlay M. C. Lin

24. Boolean Operations • Let P1, P2 be two polygons with n1 and n2 vertices respectively; and let n = n1 + n2 • Their boolean operations (intersection, union, and difference) can each be computed in O(n log n + k log n) time, where k is the complexity of the output M. C. Lin