Recall: breadth-first search, step by step

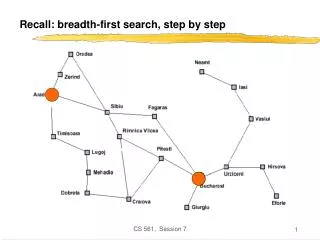
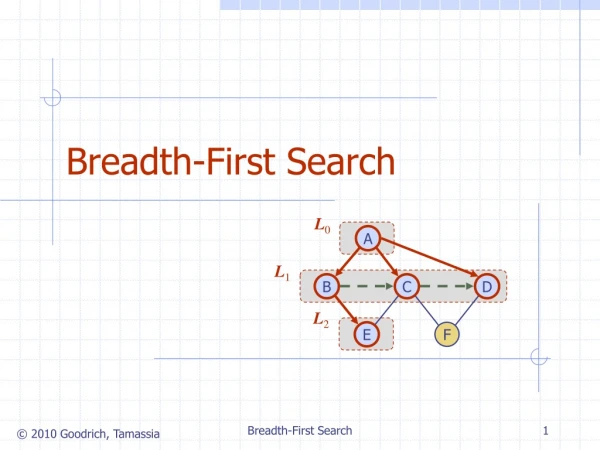
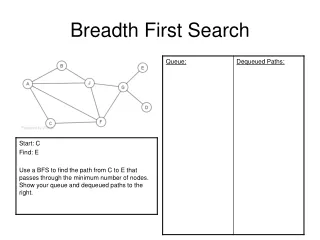
1. Recall: breadth-first search, step by step CS 561, Session 7

2. Implementation of search algorithms Function General-Search(problem, Queuing-Fn) returns a solution, or failure nodes  make-queue(make-node(initial-state[problem])) loop do if nodes is empty then return failure node  Remove-Front(nodes) if Goal-Test[problem] applied to State(node) succeeds then return node nodes  Queuing-Fn(nodes, Expand(node, Operators[problem])) end Queuing-Fn(queue, elements) is a queuing function that inserts a set of elements into the queue and determines the order of node expansion. Varieties of the queuing function produce varieties of the search algorithm. CS 561, Session 7

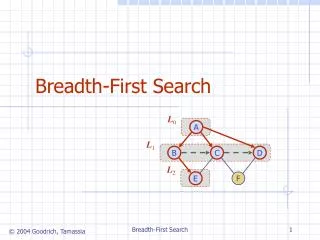
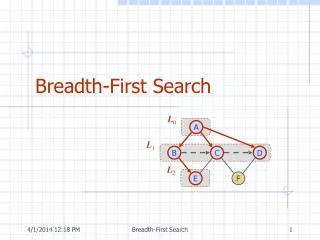
3. Recall: breath-first search, step by step CS 561, Session 7

4. Breadth-first search Node queue: initialization # state depth path cost parent # 1 Arad 0 0 -- CS 561, Session 7

5. Breadth-first search Node queue: add successors to queue end; empty queue from top # state depth path cost parent # 1 Arad 0 0 -- 2 Zerind 1 1 1 3 Sibiu 1 1 1 4 Timisoara 1 1 1 CS 561, Session 7

6. Breadth-first search Node queue: add successors to queue end; empty queue from top # state depth path cost parent # 1 Arad 0 0 -- 2 Zerind 1 1 1 3 Sibiu 1 1 1 4 Timisoara 1 1 1 5 Arad 2 2 2 6 Oradea 2 2 2 (get smart: e.g., avoid repeated states like node #5) CS 561, Session 7

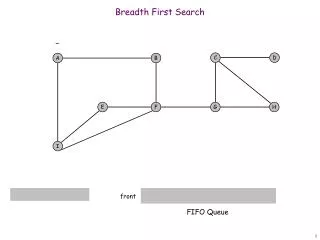
7. Depth-first search CS 561, Session 7

8. Depth-first search Node queue: initialization # state depth path cost parent # 1 Arad 0 0 -- CS 561, Session 7

9. Depth-first search Node queue: add successors to queue front; empty queue from top # state depth path cost parent # 2 Zerind 1 1 1 3 Sibiu 1 1 1 4 Timisoara 1 1 1 1 Arad 0 0 -- CS 561, Session 7

10. Depth-first search Node queue: add successors to queue front; empty queue from top # state depth path cost parent # 5 Arad 2 2 2 6 Oradea 2 2 2 2 Zerind 1 1 1 3 Sibiu 1 1 1 4 Timisoara 1 1 1 1 Arad 0 0 -- CS 561, Session 7

11. Last time: search strategies Uninformed: Use only information available in the problem formulation • Breadth-first • Uniform-cost • Depth-first • Depth-limited • Iterative deepening Informed: Use heuristics to guide the search • Best first: • Greedy search • A* search CS 561, Session 7

12. Last time: search strategies Uninformed: Use only information available in the problem formulation • Breadth-first • Uniform-cost • Depth-first • Depth-limited • Iterative deepening Informed: Use heuristics to guide the search • Best first: • Greedy search -- enfileira primeiro os nós que maximizam a “desejabilidade” heurística baseado no custo do nó corrente ao objetivo; • A* search – enfileira primeiro os nós que maximizam a soma dos custos do caminho até o nó mais o custo estimado do nó corrente ao objetivo; CS 561, Session 7

13. This time • Iterative improvement • Hill climbing • Simulated annealing CS 561, Session 7

14. Melhoria Iterativa • Em muitos problemas de otimização, o caminho é irrelevante; o estado objetivo por si só é a solução. • Então, o espaço de estados = espaço de configurações “completo”. Objetivo do algoritmo: - achar configuração ótima (ex: TSP), ou, - achar configuração que satisfaça restrições (ex: n-queens) • Em tais casos, pode-se usar algoritmos de melhoria iterativa: manter um estado “corrente” único, e tentar melhorá-lo. CS 561, Session 7

15. Exemplo de melhoria iterativa: ambiente do aspirador Ambiente simplificado: 2 localizações, cada uma pode ou não conter sujeira e pode ou não conter agente. Objetivo do agente: limpar a sujeira. Se o caminho não importa, não é necessário mante-lo (sabê-lo). CS 561, Session 7

16. Exemplo de melhoria iterativa: n-queens • objetivo: colocar n rainhas num tabuleiro nxn, sem que hajam duas rainhas na mesma linha, coluna ou diagonal. • Aqui, o estado objetivo é desconhecido inicialmente, mas é especificado por restrições que ele deve satisfazer. CS 561, Session 7

17. Hill climbing (ou descida/subida do gradiente) • Maximiza “valor” do estado corrente iterativamente, atualizando-o pelo sucessor que possui o maior valor, na medida do possível. CS 561, Session 7

18. Hill climbing • Nota: minimizar uma função “valorada” v(n) é equivalente a maximizar –v(n), então ambas noções podem ser usadas intercambeadas. • Noção de “extremização”: achar extremo (mínimo ou máximo) de uma função valorada. CS 561, Session 7

19. Hill climbing • Problema: dependendo do estado inicial, pode parar em extremo (mínimo ou máximo) local. CS 561, Session 7

20. Minimizando energia • Vamos mudar a formulação do problema um pouco, de maneira que se possa empregar um novo formalismo: - comparar o espaço de estados ao de um sistema físico sujeito a interações naturais, e - comparar a função valorada à energia potencial total (E) do sistema. • Em toda atualização, temos DE  0 • Então, a dinâmica do sistema tende a mover E de encontro ao mínimo. • Estes estados podem ser diferentes — se forem mínimos locais. Minimi- zação global pode não ser garantida. CS 561, Session 7

21. h Máquinas de Boltzmann A Máquina de Boltzmann de Hinton, Sejnowski, e Ackley (1984) usa Simulated Annealing para fugir de mínimos locais. Para motivar a solução, considere como alguém poderia fazer uma bola navegar ao longo de uma curva para “provavelmente finalizar” no local mais profundo. A idéia é “chacoalhar” a caixa próximo de h de modo que a bola pule, provavelmente, D para C, ou, dependendo da amplitude, de D para B. No final, em algum tempo a bola deverá terminar no vale C. CS 561, Session 7

22. Idéia básica do Simulated annealing • Do estado corrente tomar um estado sucessor de forma aleatórea; • Se este estado possuir valor melhor que o do estado corrente, então “aceite a transição”, ou seja, faça do estado sucessor o corrente; • Caso contrário, não desistir, aceite a transição com uma dada probabilidade (pequena na medida que o sucessor for ruim). • Algumas vezes, a função valor é não-otimizada com probabilidade diferente de zero. CS 561, Session 7

23. Analogia: Refrigerar lentamente um líquido • Quanto menor a taxa de variação de T no início, mais gradualmente o líquido se tornará gelo; • Se no início tiver mudanças bruscas em T, algumas regiões gelarão primeiro que outras CS 561, Session 7

24. Teoria estatística dos gazes, de Boltzmann • Na teoria estatística dos gases, o gás é descrito pela probabilidade de ele se encontar em estados diferentes e não por uma dinâmica determinística. • No século 19, o físico Ludwig Boltzmann desenvolveu uma teoria que incluiu uma distribuição probabilística da temperatura, isto é, regiões do gás pequenas, vizinhas, possuem a mesma energia cinética. • A idéia de Hinton, Sejnowski e Ackley’s é que esta distribuição pode ser tb usada para descrever interações neurais, onde temperatura a baixar T é atualizada por um pequeno sinal de ruído: o análogo neural do movimento aleatório termal de moléculas. Os resultados se aplicam a otimização usando redes neurais, mas a idéia é mais geral. CS 561, Session 7

25. Distribuição de Boltzmann • Em equilíbrio térmico a uma temperatura T, a distribuição de Boltzmann produz a probabilidade relativa de que o sistema ocupará o estado A versus o estado B como: • onde E(A) e E(B) são as energias associadas com os estados A e B. CS 561, Session 7

26. Simulated annealing Kirkpatrick et al. 1983: • Simulated annealing é um método geral para produzir um provável escape de mínimos locais permitindo saltos com energias mais altas. • A analogia aqui é com o processo de recozimento usado por um artesão para forjar uma espada de uma liga. • Aquece o metal, a seguir refrigera-o lentamente enquanto martela a lâmina para obter a forma desejada. • Se refrigerar a lâmina muito rapidamente, o metal formará pedaços com composição diferente; • Se o metal for refrigerado lentamente enquanto dando forma, os metais constituintes formarão uma liga uniforme. CS 561, Session 7

27. Simulated annealing na prática • determina T inicial (temperatura) • otimiza para o dado T • abaixa T (see Geman & Geman, 1984) • repete CS 561, Session 7

28. Simulated annealing na prática • determina T inicial (temperatura) • otimiza para o dado T • abaixa T (see Geman & Geman, 1984) • repete • Geman & Geman (1984): se T é abaixado lentamente (com respeito ao número de iterações usadas para otimizar a uma dada temperatura T), garante-se que o simulated annealing acha o mínimo global. • Caveat: este algoritmo pode não ter fim. O decrescimento em T (Geman & Geman) é da ordem de 1/log do número de iterações, então, T poderá nunca ser zero). Isto pode levar a um tempo infinito para atingir o mínimo global. CS 561, Session 7

29. Algoritmo para o Simulated annealing • Idéia: Escapar extremo local permitindo “movimentos ruins”, mas gradualmente decrementando o seu tamanho e freqüência. Nota: objetivo aqui é maximizar E. - CS 561, Session 7

30. Algoritmo para o Simulated annealing • Idéia: Escapar extremo local permitindo “movimentos ruins”, mas gradualmente decrementando o seu tamanho e freqüência. Algoritmo visando minimizar E. - < - CS 561, Session 7

31. Simulated annealing: casos limites • Distribuição de Boltzmann: aceita “movimento ruim” com E<0 (objetivo é maximizar E) com probabilidade P(E) = exp(E/T) • P/ T grande : E < 0 E/T < 0 and very small exp(E/T) close to 1 accept bad move with high probability • P/ T pequeno (0): E < 0 E/T < 0 and very large exp(E/T) close to 0 accept bad move with low probability CS 561, Session 7

32. Simulated annealing: casos limites • Distribuição de Boltzmann: aceita “movimento ruim” com E<0 (objetivo é maximizar E) com probabilidade P(E) = exp(E/T) • If T is large: E < 0 E/T < 0 and very small exp(E/T) close to 1 accept bad move with high probability • If T is near 0: E < 0 E/T < 0 and very large exp(E/T) close to 0 accept bad move with low probability Random walk Deterministic down-hill CS 561, Session 7

33. Sumário • Best-first search = general search, onde os nós de custo mínimo (de acôrdo com alguma medida) são expandidos primeiro. • Greedy search = best-first com o custo estimado para alcançar o objetivo sendo uma medida heurística. - Geralmente mais rápido que uninformed search - não ótimo - não completo. • A* search = best-first com medida = custo efetivo até o nó (desde origem) + custo estimado até o objetivo. - combina vantagens das estratégias uniform-cost e greedy - completo, ótimo e otimamente eficiente - complexidade de memória ainda exponencial CS 561, Session 7

34. Sumário • Complexidade de tempo dos algoritmos heurísticos dependem da qualidade da função heurística. Boas heurísticas podem algumas vezes serem construídas examinando-se a definição do problema ou generalizando de experiências com a classe de problemas. • Algoritmos de melhoria iterativa mantém apenas um único estado em memória. • Podem parar em extremos locais; simulated annealing provê uma maneira de escapar de extremos locais, e é completo e ótimo, se for aplicado um resfriamento suficientemente lento. CS 561, Session 7