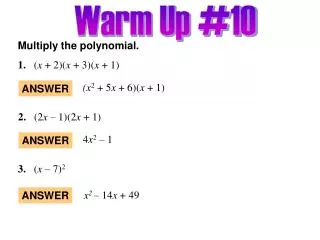1 / 16

Factoring Polynomials: Techniques and Guided Practice

This comprehensive guide covers the methods for factoring various polynomials, including finding common monomial factors, applying the difference of squares, and factoring perfect square trinomials. Each example walks through the steps necessary to factor completely, including guided practice problems to reinforce learning. The material is designed for students to master polynomial factoring techniques, ensuring a solid understanding of algebraic concepts. This resource includes examples, practice problems, and clear explanations for effective learning.

amal-riggs
Télécharger la présentation

Factoring Polynomials: Techniques and Guided Practice

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Warm Up #10 Multiply the polynomial. 1. (x + 2)(x + 3)(x + 1) (x2 + 5x + 6)(x + 1) ANSWER 2. (2x– 1)(2x + 1) 4x2– 1 ANSWER 3. (x – 7)2 x2 – 14x + 49 ANSWER

  2. Check HW 5.3

  3. EXAMPLE 1 Find a common monomial factor Factor the polynomial completely. a. x3 + 2x2 – 15x = x(x2 + 2x – 15) Factor common monomial. = x(x + 5)(x – 3) Factor trinomial. = 2y3(y2 – 9) b. 2y5 – 18y3 Factor common monomial. = 2y3(y + 3)(y – 3) Difference of two squares = 4z2(z2 – 4z + 4) c. 4z4 – 16z3 + 16z2 Factor common monomial. = 4z2(z – 2)2 Perfect square trinomial

  4. Sum and Difference of Cubes:

  5. Apply the rule for sum of cubes: Write each monomial as a cube and apply either of the rules. Rewrite as cubes

  6. Apply the rule for difference of cubes: Rewrite as cubes

  7. for Examples 1 and 2 GUIDED PRACTICE Factor the polynomial completely. 2. 3y5 – 75y3 1.x3 – 7x2 + 10x

  8. for Examples 1 and 2 GUIDED PRACTICE Factor the polynomial completely. 3. 16b5 + 686b2 2b2(2b + 7)(4b2 –14b + 49)

  9. for Examples 1 and 2 GUIDED PRACTICE Factor the polynomial completely. 4. w3 – 27 (w – 3)(w2 + 3w + 9)

  10. Factor by Grouping EXAMPLE 3 Factor the polynomial x3 – 3x2 – 16x + 48 completely. = x2(x – 3) –16(x – 3) x3– 3x2– 16x + 48 Factor by grouping. = (x2– 16)(x – 3) Distributive property = (x+ 4)(x – 4)(x – 3) Difference of two squares

  11. Factor polynomials in quadratic form EXAMPLE 4 Factor completely:(a) 16x4 – 81and(b) 2p8 + 10p5 + 12p2. a. 16x4 – 81 = (4x2)2 – 92 Write as difference of two squares. = (4x2 + 9)(4x2 – 9) Difference of two squares = (4x2 + 9)(2x + 3)(2x – 3) Difference of two squares Factor common monomial. b. 2p8 + 10p5 + 12p2 = 2p2(p6 + 5p3 + 6) Factor trinomial in quadratic form. =2p2(p3 + 3)(p3 + 2)

  12. for Examples 3 and 4 GUIDED PRACTICE Factor the polynomial completely. 5. x3 + 7x2 – 9x – 63 ANSWER (x+ 3)(x – 3)(x + 7)

  13. for Examples 3 and 4 GUIDED PRACTICE Factor the polynomial completely. 6. 16g4 – 625 (4g2 + 25)(2g + 5)(2g – 5) ANSWER

  14. for Examples 3 and 4 GUIDED PRACTICE Factor the polynomial completely. 7. 4t6 – 20t4 + 24t2 4t2(t2 – 3)(t2 – 2 ) ANSWER

  15. Class/Homework AssignmentWorkbook 5.4 (multiples of 3)

More Related