1 / 22

Calculating Perimeter and Angles in Geometry Problems

In this geometry-focused review, we tackle problems involving triangles, angles, and teams competing in a basketball-themed game. The first problem requires finding the perimeter of a 30°-60°-90° triangle with a shorter leg of 7.4 meters. Additional tasks include determining angle relationships in right triangles, using sine, cosine, and tangent ratios, and solving for unknown values such as lengths and angles. This engaging approach not only reinforces mathematical concepts but also integrates a fun, competitive element.

anika
Télécharger la présentation

Calculating Perimeter and Angles in Geometry Problems

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

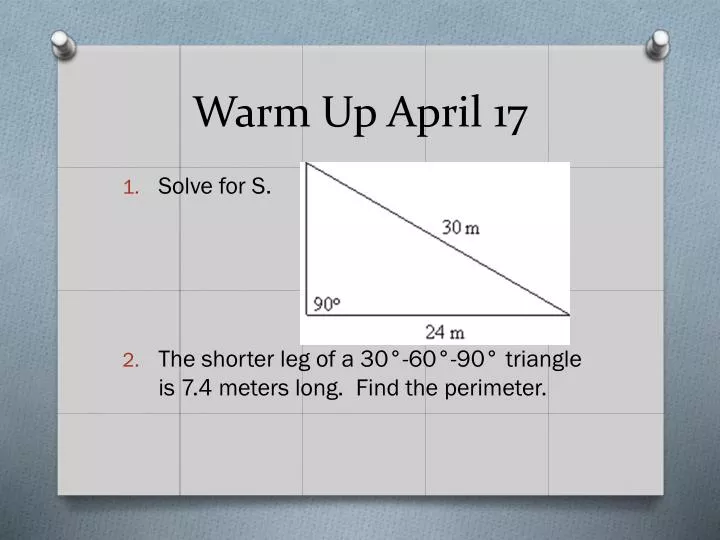
  1. Warm Up April 17 • Solve for S. • The shorter leg of a 30°-60°-90° triangle is 7.4 meters long. Find the perimeter.

  2. EOCT Week 13 #4

  3. HW ?s

  4. Review Basketball

  5. We are going to divide into two teams. Each team will send a player up to the board to answer the question. The team that gets the answer correct first will have a chance to shoot for a point The team with the most correct will win.

  6. 1. • Angle A and angle B are complementary angles in a right triangle. The value of sin A is . What is the value of tan B?

  7. The balloon is 250ft away from the Tripod. Solve for h. 2.

  8. Solve for X and Y

  9. Solve for X and Y

  10. What is the length of LP?

  11. Find the angle of A

  12. Find X

  13. What is the length of the ladder?

  14. sin J is 15/17 . What is the value of the cos J?

  15. Solve for X and Y

  16. Find X and Y

  17. Find X and Y

  18. Solve for X

  19. Solve for X

  20. Solve for C

  21. Solve for a

  22. 1. tanB = 12/5 2. 212.8 3. x= 12.8, y=5.7 4. x= 29.4, y=45.7 5. 11 6. 36.8 7. 57.9 8. 35.1 9. 8/17 10. x= 4, y= 10 11. x=10, y= 10 12. x= 10, y= 20 13. 14. 37 15. 51 16. 6

More Related