Taylor
60 likes | 290 Vues
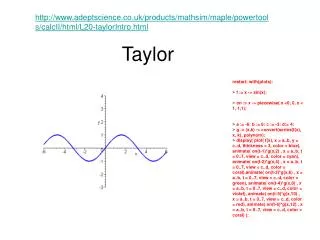
http://www.adeptscience.co.uk/products/mathsim/maple/powertools/calcII/html/L20-taylorIntro.html. Taylor. restart; with(plots): > f := x -> sin(x); > on := x -> piecewise( x <0, 0, x < 1, 1,1); > a := -6: b := 6: c := -3: d:= 4: > g := (x,k) -> convert(series(f(x), x, k), polynom):

Taylor
E N D
Presentation Transcript
http://www.adeptscience.co.uk/products/mathsim/maple/powertools/calcII/html/L20-taylorIntro.htmlhttp://www.adeptscience.co.uk/products/mathsim/maple/powertools/calcII/html/L20-taylorIntro.html Taylor restart; with(plots): > f := x -> sin(x); > on := x -> piecewise( x <0, 0, x < 1, 1,1); > a := -6: b := 6: c := -3: d:= 4: > g := (x,k) -> convert(series(f(x), x, k), polynom): > display( plot( f(x), x = a..b, y = c..d, thickness = 3, color = blue), animate( on(t-1)*g(x,2) , x = a..b, t = 0..7, view = c..d, color = cyan), animate( on(t-2)*g(x,4) , x = a..b, t = 0..7, view = c..d, color = coral),animate( on(t-3)*g(x,6) , x = a..b, t = 0..7, view = c..d, color = green), animate( on(t-4)*g(x,8) , x = a..b, t = 0..7, view = c..d, color = violet), animate( on(t-5)*g(x,10) , x = a..b, t = 0..7, view = c..d, color = red), animate( on(t-6)*g(x,12) , x = a..b, t = 0..7, view = c..d, color = coral) );
Taylor Polynomials--A Visual Approach to Approximations http://mathdemos.gcsu.edu/TaylorPolynomials/
Approximation to f(x) = cos(x) by Maclaurin Polynomials and the error. http://mathdemos.gcsu.edu/TaylorPolynomials/
Approximation to f(x) = log(x+1) by Maclaurin Polynomials and the error.
http://mathdemos.gcsu.edu/TaylorPolynomials/gallery/index.htmlhttp://mathdemos.gcsu.edu/TaylorPolynomials/gallery/index.html
http://mathdemos.gcsu.edu/TaylorPolynomials/gallery/index.htmlhttp://mathdemos.gcsu.edu/TaylorPolynomials/gallery/index.html