1 / 54

Numerical Methods Root Finding Secant Method Modified Secant False Position Method Newton Method

4. Numerical Methods Root Finding Secant Method Modified Secant False Position Method Newton Method. Root Finding. False Position Method. The False-Position Method ( Regula-Falsi ). We can approximate the solution by doing a linear interpolation between f(x u ) and f(x l )

astromberg
Télécharger la présentation

Numerical Methods Root Finding Secant Method Modified Secant False Position Method Newton Method

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 4 Numerical Methods Root Finding Secant Method Modified Secant False Position Method Newton Method

  2. Root Finding False Position Method

  3. The False-Position Method (Regula-Falsi) • We can approximate the solution by doing a linear interpolation between f(xu) and f(xl) • Find xr such that l(xr)=0, where l(x) is the linear approximation of f(x) between xl and xu • Derive xr using similar triangles

  4. Based on similar triangles next estimate, xr f(xu) xl xu f(xl)

  5. Example

  6. Example Determine the root of the following equation using the false position method starting with an initial estimate of xl=4.55 and xu=4.65 f(x) = x3 - 98

  7. Pitfalls of False Position Method

  8. Bisection Method (Converge quicker) • False-position Method

  9. 2 2 1 1 Comparison of False Position and Secant Method f(x) f(x) x x new est. new est.

  10. Secant method

  11. Secant method

  12. Secant method Select two estimates. Note: f(xi) and f(xi+1) are not opposite signs. f(x) { x initial estimates

  13. Secant method f(x) slope between two estimates { x initial estimates

  14. Secant method f(x) slope between two estimates { x initial estimates new estimate

  15. To get xn+1 from xn and xn-1 we write out the equation of the secant line and using the points xn and xn-1. We then plug in the point (xn+1,0) and solve for xn+1. equation of secant substitute (xn+1,0) solve for xn+1 xn+1=h(xn-1,xn) The equation above gives the recursively defined sequence for xn. This is what is used for the Secant Method. The halting condition is usually given by the Standard Cauchy Error.

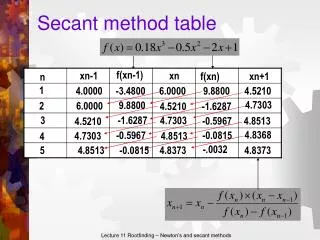
  16. Secant method table f(xn-1) xn-1 xn f(xn) xn+1 n 1 4.0000 -3.4800 6.0000 9.8800 4.5210 4.7303 9.8800 2 6.0000 4.5210 -1.6287 -1.6287 3 4.7303 -0.5967 4.8513 4.5210 4.8368 -0.5967 -0.0815 4.8513 4.7303 4 -.0032 5 4.8513 4.8373 -0.0815 4.8373

  17. Secant Illustration F(x) = x2 - 10 • 1 (a=1, fa=-9) (b=10, fb=90) •  int = 1.8, fint = -6.7 • 2(a=10, fa=90) (b=1.8, fb= -6.7) • int = 0.88, fint = -9.22 3 (a=1.8, fa=-6.7) (b=0.88, fb=-9.22) • int = 4.25, fint = 8 4 (a=0.88, fa=-9.22) (b=4.25, fb=8) • Int =2.68, fint = -2.8 Etc… 2 3 1 4

  18. Example Determine the root of f(x) = e-x - x using the secant method. Use the starting points x0 = 0 and x1 = 1.0.

  19. Solution • Choose two starting points • x0 = 0 f(x0 ) =1 • x1 = 1.0 f(x1) = -0.632 • Calculate x2 • x2 = 1 - (-0.632)(0 - 1)/(1+0.632) = 0.6127

  20. Solution • Second iteration • x1 = 1.0 f(x1) = -0.632 • x2 = 0.613 f(x2) = -0.0708 • NOTE: f(x) are the same sign. OK here. • x3 = 0.613 - (-0.0708)(1-0.613)/(-0.632+0.0708) • x3 = 0.564 f(x3) = 0.0052 • ea = abs[(0.564-0.613)/(0.564)] x 100 = 8.23%

  21. Solution • Third iteration • x2 = 0.613 f(x2) = -0.0708 • x3 = 0.564 f(x3) = 0.0052 • x4 = 0.567 f(x4) = -0.00004 • ea = 0.59% et = 0.0048% • Know the difference between these error terms

  22. double secant(double c, int iterations, double tol)… for ( int i = 0; i < iterations; i++) { double x = ( fa*b - fb*a ) / ( fa - fb ); double fx = func( x, c ); if ( fabs( fx ) < tol ) return x; a = b; fa = fb; b = x; fb = fx; } return -1; SECANT METHOD The change from ordinary regula is that the sign check is dropped and points are just “shifted over”

  23. Example

  24. Ex. • Use secant method to estimate the root of f(x) = ln x. • Start the computation with value of • xl = xi-1 = 0.5 • xu = xi = 5.0 • Solution The secant method

  25. Problems With the Secant Method • The number of iterations required can not be determined before the algorithm begins. • The algorithm will halt (program termination by division by zero if not checked for) if a horizontal secant line is encountered. • The secant method will sometimes find an extraneous root.

  26. Modified Secant Method

  27. Modified Secant Method Original Secant Method Modified Secant Method

  28. Ex. • Use the secant method to estimate the root of f(x) = e-x – x. Use a value of 0.01 for  and start with x0 = 1.0. • Solution (true root = 0.56714329…) • First iteration • x0 = 1 f(x0) = -0.63212 • x1+ x0 = 1.01 f(x1+ x0) = -0.64578 • Calculate t = 5.3%

  29. Applied Problem You buy a $20 K piece of equipment for nothing down and $5K per year for 5 years. What interest rate are you paying? The formula relating present worth (P), annual payments (A), number of years (n) and the interest rate (i) is:

  30. Root Finding Newton Method

  31. Newton’s Method • Open solution, that requires only one current guess. • Root does not need to be bracketed. • Consider some point x0. • If we approximate f(x) as a line about x0, then we can again solve for the root of the line.

  32. tangent f(xi) xi xi+1 Newton Raphson

  33. Newton’s Method (cont) • Derived using Taylor’s expansion

  34. Newton’s Method • Solving, leads to the following iteration:

  35. Newton RaphsonPitfalls solution diverges f(x) (x)

  36. Finding a square-root • Example: 2 = 1.4142135623730950488016887242097 • Let x0 be one and apply Newton’s method.

  37. Finding a square-root • Example: 2 = 1.4142135623730950488016887242097 • Note the rapid convergence • Note, this was done with the standard Microsoft calculator to maximum precision.

  38. Newton’s method

  39. Example Use the Newton Raphson method to determine the root of f(x) = x2 - 11 using an initial guess of xi = 3

  40. Solution • f(x) = x2 - 11 • f '(x) = 2x • initial guess xi = 3 • f(3) = -2 • f '(3) = 6

  41. Solution In this method, we begin to use a numbering system: x0 = 3 x1 = 3.33 Continue to determine x2, x3 etc.

  42. Solution

  43. Example: Newton’s Method • f(x)= x3–3x2 –x+9=0 Worse than bisection !?

  44. Newton’s Algorithm • Requires the derivative function to be evaluated, hence more function evaluations per iteration. • A robust solution would check to see if the iteration is stepping too far and limit the step. • Most uses of Newton’s method assume the approximation is pretty close and apply one to three iterations blindly.

  45. Division by Multiplication • Newton’s method has many uses in computing basic numbers. • For example, consider the equation: • Newton’s method gives the iteration:

  46. Quadratic Convergence of Newton • Let x* be the converged solution • Recall

  47. Quadratic Convergence of Newton (cont) • Subtracting x*: Or we say Newton’s method has quadratic convergence

  48. Applied Problem The concentration of pollutant bacteria C in a lake decreases according to: Determine the time required for the bacteria to be reduced to 10 ppm.

  49. Roots of Equations Chemical Engineering (C&C 8.1, p. 187): van der Waals equation; v = V/n (= volume/# moles) Find the molal volume v such that p = pressure, T = temperature, R = universal gas constant, a & b = empirical constants

  50. Roots of Equations • Civil Engineering (C&C Prob. 8.17, p. 205): • Find the horizontal component of tension, H, in a cable that passes through (0,y0) and (x,y) w = weight per unit length of cable

More Related