1 / 12

Multilevel thresholding by fast PNN based algorithm

Multilevel thresholding by fast PNN based algorithm. Olli Virmajoki and Pasi Fränti. UNIVERSITY OF JOENSUU DEPARTMENT OF COMPUTER SCIENCE FINLAND. Multi-level thresholding. Given image with N input values, threshold the image into M values.

bisa
Télécharger la présentation

Multilevel thresholding by fast PNN based algorithm

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Multilevel thresholding by fast PNN based algorithm Olli Virmajoki and Pasi Fränti UNIVERSITY OF JOENSUU DEPARTMENT OF COMPUTER SCIENCE FINLAND

  2. Multi-level thresholding • Given image with N input values, threshold the image into M values. • Considered as algorithmic problem: given a minimization criterion (MSE), find optimal thresholds.

  3. Optimal thresholding • Optimal thresholding by exhaustive search in O(NM-1) time [Otsu 1979]. • Medical images can have 16 bpp. Exhaustive search takes ~6553610. • Sub-optimal methods: Lloyd-Max quantizer with O(N)time.

  4. Pairwise Nearest Neighbor method (PNN) • New multilevel thresholding algorithm based on the pairwise nearest neighbor (PNN). • PNN used in vector quantization (Equitz 1989) but considered slow: • Original method takes O(N3), • Kurita’s method takes O(N2 log N) • Using Nearest neighbor pointers: O(N2). • PNN is lower limited by (N2) • Our contribution: To show that PNN can be implemented in O(N log N) time !!!

  5. PNN algorithm SET m=N (N-1 thresholds) REPEAT • Find threshold to be removed: O(N) • Remove threshold: O(1) • Update the class parameters: O(1) • SET m=m-1 UNTIL m=M

  6. PNN with heap structure

  7. Time complexity

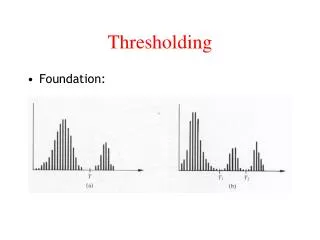
  8. Histograms of test images 8 bpp 12 bpp 16 bpp

  9. Methods in comparison • Uniform quantizer (UQ) • LMQ • PNN • PNN + LMQ • Optimal (Otsu’s method)

  10. MSE comparison (Medical3) 1. MSE values significantly smaller than Uniform Quantizer 3. PNN+LMQ values can be significantly smaller than LMQ alone 2. PNN+LMQ gives near-optimal results (for small M values)

  11. Time Comparison (Medical3) • All sub-optimal methods are fast 2. Optimal thresholding is too slow for larger M values.

  12. Conclusions • Fast PNN-based O(N log N) time algorithm for multilevel non-parametric thresholding. • Considerably faster than optimalthresholding. • Better quality than the Lloyd-Max quantizer alone.

More Related