1 / 8

14.3 Trigonometric Identities

Understand Trigonometric Identities to simplify expressions effortlessly. Learn to apply Quotient, Reciprocal, and Pythagorean Identities to solve equations effectively. Practice examples to enhance your skills further.

caseyj
Télécharger la présentation

14.3 Trigonometric Identities

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 14.3 Trigonometric Identities Objectives: Use identities to find trig values Use trig identities to simplify expressions.

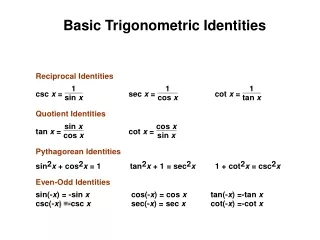
  2. Trig Identities Trig identity – an equation involving trig functions that is true for all values for which every expression in the equation is defined. Quotient Identities: Reciprocal Identities:

  3. Pythagorean Identities They may also be solved for any part of the equation. (cos²θ=1-sin²θ)

  4. Using trig identities The trig identities can be used to find values of other functions by plugging what is given into the appropriate identity and solving for that function. Keep in mind the sign of the value in the quadrant specified. Example: Find tan θ if sec θ=-2 and 180°<θ<270° We know it’s in the 3rd quadrant and tan is positive. Use tan²θ+1=sec²θ tan²θ+1=(-2)² tan²θ+1=4 tan²θ=3

  5. Another Example Find sin θ if cosθ=-½ and 90°<θ<180° Quadrant: II, so sin is pos. in 2nd quadrant cos²θ+sin²θ=1 (-½)²+sin²θ=1 ¼+sin²θ=1 sin²θ=1-¼

  6. Simplifying expressions You can use the identities to simplify expressions. Example: Simplify sinθ(cscθ-sinθ)

  7. Another example Simplify

  8. Homeworkp 77914-32 even

More Related