1 / 21

8.4 Logarithms

This resource provides a comprehensive overview of evaluating logarithms and their relationship with exponential functions. Learn how to convert between exponential and logarithmic forms, understand the concept of common and natural logarithms, and use calculators for evaluation. The guide also includes practical examples to enhance your understanding of logarithmic expressions, including common bases like 10 and natural base e. Master the techniques for simplifying and solving logarithmic equations effectively.

catori
Télécharger la présentation

8.4 Logarithms

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 8.4 Logarithms p. 486

  2. Daily Question: How do you evaluate a logarithm?

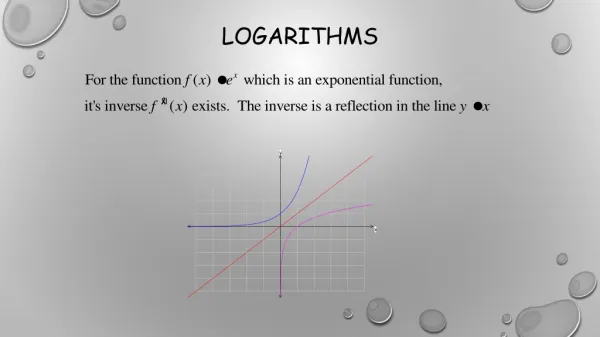
  3. Logarithmic Function The inverse of an exponential function is a logarithmic function. x = log b y read: “x equals log base b of y”

  4. y = bx x = logby We can convert exponential equations to logarithmic equations and vice versa, using this: These two equations are equivalent

  5. y = bx x = logby Exponential form logarithmic form

  6. where y > 0 b > 0 b 1 unknown If y = bx then x = logby base base Another way to “read” logs: “What is the exponent of b that gives you y?” technical stuff

  7. “What is the exponent of 3 that gives you 5?” Convert to exponential form 1) 2) 3)

  8. Convert to logarithmic form 4) 5) 6)

  9. Now that we can convert between the two forms we can simplify logarithmic expressions.

  10. “What is the exponent of that gives you 32?” Simplify 7) log2 32 2? = 32 ? = 5 “What is the exponent of 3 that gives you 27?” 8) log3 27 3? = 27 ? = 3 9) log4 2 4? = 2 ? = 0.5 10) log3 1 3? = 1 ? = 0

  11. Evaluate try:

  12. Common Logarithm • A common logarithm is a logarithm that is base 10. • When a logarithm is base 10, we don’t write the base. log10 = log • We like base 10 because we can evaluate it in our calculator. (Use the LOG button)

  13. Common logs and natural logs with a calculator log10 button ln button

  14. Evaluate with a calculator = 1 11) log10 10 = 0.7959 12) 2 log10 2.5 no solution 13) log10 (-2) Remember this means 10? = -2

  15. Try these using your calculators: • 10x = 85 • 10x = 1.498 • 10x = -5.5

  16. Natural Exponential Function y = ex Natural Base ln e = 1

  17. Natural Logarithmic Function y = ex x = loge y x = ln y the natural logarithmic function is the inverse of the natural exponential function

  18. Convert to natural logarithmic form: a. 10 = ex b. 14 = e 2x Convert to natural exponential form: a. ln 4 = 1.386… b. ln 6 = 1.792…

  19. Evaluate: ln x a. x = 2 b. x = ½ c. x = -1 .693 -0.693 undefined

  20. Solving natural bases 1.) ex+7 = 98 2.) 4e3x-5 = 72 3.) ln x3 - 5 = 1

  21. page 490 #16-64 x4 Homework

More Related