Stack
260 likes | 652 Vues
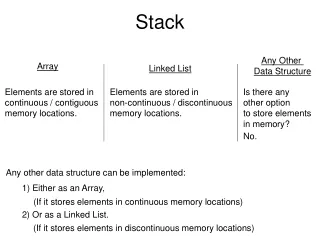
Stack. Stack ADT. A stack is an abstract data type based on the list data model All operations are performed at one end of the list called the top of the stack (TOS) “LIFO (for last-in first-out) list” is a synonym for stack Common operations: push(x) puts the element x on top of the stack

Stack
E N D
Presentation Transcript
Stack ADT • A stack is an abstract data type based on the list data model • All operations are performed at one end of the list called the top of the stack (TOS) • “LIFO (for last-in first-out) list” is a synonym for stack • Common operations: • push(x) puts the element x on top of the stack • pop removes the topmost element from the stack.
Java Stack Interface • public interface Stack { • public void push(Object x); • public Object pop(); • public Object peek(); • public boolean isEmpty(); • public void clear(); • }
From interface to implementation • Given that we want to support some interface, the designer still faces a choice • What will be the best way to implement this interface for my expected type of use? • Choice of implementation can reflect many considerations • Major factors we think about • Speed for typical use case • Storage space required
index 4 Array implementation of Stack class ArrayStack implements Stack { private Object[] array; //Array that holds the Stack private int index = 0; //First empty slot in Stack public ArrayStack(int maxSize) { array = new Object[maxSize]; } public void push(Object x) { array[index++] = x; } public Object pop() { return array[--index]; } public Object peek() { return array[index-1]; } public boolean isEmpty() { return index == 0; } public void clear() { index = 0; } } max-1 3 2 1 0 O(1) worst-case time for each operation Question: What can go wrong? …. What if maxSize is too small?
head Linked List Implementation of Stack class ListStack implements Stack { private Node head = null; //Head of list that //holds the Stack public void push(Object x) { head = new Node(x, head); } public Object pop() { Node temp = head; head = head.next; return temp.data; } public Object peek() { return head.data; } public boolean isEmpty() { return head == null; } public void clear() { head = null; } } O(1) worst-case time for each operation (but constant is larger) Note that array implementation can overflow, but the linked list version cannot
Use of Stack • Infix to postfix conversion • Postfix evaluation • Function calls • etc
Infix to postfix • When an operand is read, output it • When ) is read, push it • When an operator is read: • If TOS item has higher or equal precedence, repeatedly pop until TOS has an element of lower precedence or stack empty, then push the operator • If the stack is empty or TOS item has lower precedence, just push it • When ) is found, pop until we find the matching ( • ( has the lowest precedence when in the stack but has the highest precedence when in the input • When we reach the end of input, pop until the stack is empty
Example • Refer to the slides by Otávio Braga linked from the class website
Postfix evaluation • Starting with an empty stack, we scan the postfix expression from left to right • Each time we encounter an argument, we push it onto the stack • When we encounter an operator, we pop the stack twice, remembering the operands popped • We then apply the operator to the two popped values (with the second as the left operand) and push the result onto the stack
Example • Evaluating 3 4 + 2 *
Postfix to Expression Tree A 2 * 2 A * B * - B 2 * + A B - / Push A Push 2 Pop 2 Pop A Create tree_1 Push tree_1 Push 2 Push A Pop A Pop 2 Create tree_2 Push tree_2 Push B Pop B Pop tree_2 Create tree_3 Push tree_3 Pop tree_3 Pop tree_1 Create tree_4 Push tree_4 Push B Push 2 Pop 2 Pop B Create tree_5 Push tree_5 Pop tree_5 Pop tree_4 Create tree_6 Push tree_6 Push A Push B Pop B Pop A Create tree_7 Push tree_7 Pop tree_7 Pop tree_6 Create tree_8 Push tree_8 tree_8 tree_6 tree_7 tree_4 tree_5 tree_1 tree_3 tree_2
Evaluating expression tree • If at leaf node (operand node) return the operand’s value • Otherwise: • Evaluate the left sub-tree • Evaluate the right sub-tree • Combine the results from both sub-trees with the operator at root public static int eval(TreeCell root) { int left_result, right_result; if (root.datum is operand) return operand’s value; left_result = eval(root.left); right_result = eval(root.right); switch (root.datum) { case + : return left_result + right_result; case * : return left_result * right_result; : : } }
Function calls • An important application of stacks is normally hidden from view • A stack is used to allocate space in the computer’s memory to the variables belonging to the various functions of a program • Example: a recursive factorial function • Has a parameter n and a return value • As fact calls itself recursively, different calls with different parameter are active at the same time • A frame for each call is created and place on TOS • When a given call return, its frame gets popped off
public static int factorial(int 3) { int fact; if (n > 1) fact = factorial(2) * 3; else fact = 1; return fact; }
public static int factorial(int 3) { int fact; if (n > 1) fact = factorial(2) * 3; else fact = 1; return fact; } public static int factorial(int 2) { int fact; if (n > 1) fact = factorial(1) * 2; else fact = 1; return fact; }
public static int factorial(int 3) { int fact; if (n > 1) fact = factorial(2) * 3; else fact = 1; return fact; } public static int factorial(int 2) { int fact; if (n > 1) fact = factorial(1) * 2; else fact = 1; return fact; } public static int factorial(int 1) { int fact; if (n > 1) fact = factorial(n - 1) * n; else fact = 1; return fact; }
public static int factorial(int 3) { int fact; if (n > 1) fact = factorial(2)* 3; else fact = 1; return fact; } public static int factorial(int 2) { int fact; if (n > 1) fact = factorial(1)* 2; else fact = 1; return fact; } public static int factorial(int 1) { int fact; if (n > 1) fact = factorial(n - 1) * n; else fact = 1; return 1; }
public static int factorial(int 3) { int fact; if (n > 1) fact = factorial(2)* 3; else fact = 1; return fact; } public static int factorial(int 2) { int fact; if (n > 1) fact = 1* 2; else fact = 1; return fact; } public static int factorial(int 1) { int fact; if (n > 1) fact = factorial(n - 1) * n; else fact = 1; return 1; }
public static int factorial(int 3) { int fact; if (n > 1) fact = factorial(2)* 3; else fact = 1; return fact; } public static int factorial(int 2) { int fact; if (n > 1) fact = 1* 2; else fact = 1; return 2; }
public static int factorial(int 3) { int fact; if (n > 1) fact = 2* 3; else fact = 1; return fact; } public static int factorial(int 2) { int fact; if (n > 1) fact = 1* 2; else fact = 1; return 2; }
public static int factorial(int 3) { int fact; if (n > 1) fact = 2*3; else fact = 1; return 6; }