1 / 14

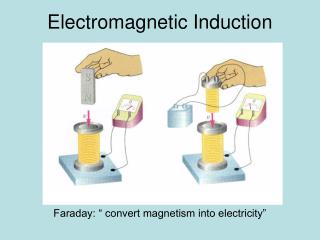
Electromagnetic Induction

Electromagnetic Induction. Chapter 22. 22.1 induced EMF and Induced Current. If a coil of conducting material and a magnet are moving (relative to one another) an electric current can be induced . The changing magnetic field forces the electrons to move one direction or another.

denise
Télécharger la présentation

Electromagnetic Induction

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Electromagnetic Induction Chapter 22

  2. 22.1 induced EMF and Induced Current • If a coil of conducting material and a magnet are moving (relative to one another) an electric current can be induced. • The changing magnetic field forces the electrons to move one direction or another. • Since a source of emf is needed to produce a current, the coil itself behaves as if it were a source of emf; in this case an induced emf.

  3. How to induce emf • Move a bar magnet near a coil • Move a magnet away from a coil • Move a coil toward a magnet • Change the area of a coil in a constant magnetic field • MUST have either magnet or coil moving • MUST have a closed circuit or coil For I to exist

  4. 22.2 Motional EMF • Moving a conducting rod through a constant magnetic field can separate the positive and negative charges existing within the rod. • Once all possible charge movement has taken place, the separated charges cause an induced or motional emf. • Emf exists as long as the rod moves • Electric and magnetic forces balance at equilibrium

  5. Motional emf when v, B, and L are perpendicular • ε = 0 when v = 0m/s • ε is expressed in volts

  6. Motional EMF and Electrical Energy • Magnetic force acts on charges in a conductor → motional emf → emf causes a current → second magnetic force is created • Since emf cause a current that is perpendicular to B, a force that would slow down the rod is generated. • A counterbalancing force must be applied to the rod by an external agent.

  7. Energy from Motional EMF • The external force sill do work in such a system. • Word done is equal to the electrical energy of the bulb. • Remember: F = ILBsinθcan be used as a force in both F=ma and W = Fxcosθ. • This concept follows the law of conservation of energy.

  8. 22.3 Magnetic Flux: Motional EMF and Magnetic Flux • Magnetic Flux: product of magnetic field and area (BA) • Symbolized by Greek letter phi • Φ = BA • magnitude of the induced emf is the change in flux divided by the time interval (-) appears in this equation b/c the direction of induced I is such that magnetic F acts on the rod to oppose its motion, therefore slowing down the rod

  9. A General Expression for φ • If B or φare not constant, the average value of the product Bcosφis used to compute the flux. • Magnetic flux is proportional to the number of field lines per unit area that pass through a surface perpendicular to the lines

  10. 22.4 Faraday’s Law • All hail to Michael Faraday and Joseph Henry for discovering electromagnetic induction!!!! • When there is a change in flux through a loop of wire, and emf is induced in the loop.

  11. 22.5 Lenz’s Law • A method for determining the polarity of the induced emf is needed so that + and – terminals can be determined. • Remember, two factors contribute to the net magnetic field penetrating a coil of wire • Original magnetic field producing changing flux • Induced current creating its own magnetic field (induced magnetic field)

  12. Lenz’s Law • The induced emf resulting from a changing magnetic flux has a polarity that leads to an induced current whose direction is such that the induced magnetic field opposes the original flux change.

  13. Reasoning Strategy • Determine whether the magnetic flux that penetrates a coil is increasing or decreasing. • Find what the direction of the induced magnetic field must be so that it can oppose the change in flux by adding to or subtracting from the original field • Once direction of induced magnetic field is found, use RHR-2 to determine the direction of the induced current. Then the polarity of the induced emf can be assigned because conventional current is directed out of the positive terminal, through the external circuit, and into the negative terminal.

  14. Last minute hints • Electromagnetic induction is explained well here. • The induced field is not always opposite to the external field, because Lenz’s law requires only that is must oppose the change in the flux that generates the emf. • To oppose an increase in flux, the direction of the induced magnetic field must be opposite to the field of a bar magnet.

More Related