1 / 58

Tree

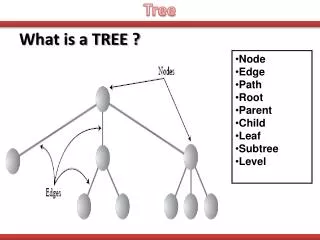
Tree. tree = connected graph with no cycle tree = connected graph with |V|-1 edges tree = graph with |V|-1 edges and no cycles. Tree. tree = connected graph with no cycle tree = connected graph with |V|-1 edges tree = graph with |V|-1 edges and no cycles.

duante
Télécharger la présentation

Tree

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Tree tree = connected graph with no cycle tree = connected graph with |V|-1 edges tree = graph with |V|-1 edges and no cycles

  2. Tree tree = connected graph with no cycle tree = connected graph with |V|-1 edges tree = graph with |V|-1 edges and no cycles no cycle  vertex of degree  1 |V|-1 edges  vertex of degree  1 connected  no vertex of degree 0 (unless |V|=1)

  3. no cycle  vertex of degree  1 Supose not, i.e., all vertices of degree  2, yet no cycle. Let v1,...,vt be the longest path vt has 2-neighbors, one different from vt-1. Why cannot take v1,...,vt,u ? Cycle. Contradiction.

  4. |V|-1 edges  vertex of degree  1 Suppose all degrees  2. Then |E|=(1/2)  deg(v)  |V| Contradiction. Done. vV

  5. connected  no vertex of degree 0 (unless |V|=1)

  6. Tree connected graph with no cycle connected graph with |V|-1 edges graph with |V|-1 edges and no cycles  no cycle  vertex of degree  1 |V|-1 edges  vertex of degree  1 connected  no vertex of degree 0 (unless |V|=1)

  7. connected graph with no cycle connected graph with |V|-1 edges   Induction on |V|. Base case |V|=1. Let G be connected with no cycles. Then G has vertex v of degree 1. Let G’ = G – v. Then G’ is connected and has no cycle. By IH G’ has |V|-2 edges and hence G has |V|-1 edges.

  8. connected graph with no cycle connected graph with |V|-1 edges   Induction on |V|. Base case |V|=1. Let G be connected |V|-1 edges. Then G has vertex v of degree 1. Let G’ = G – v. Then G’ is connected and has |V’|-1 edges. By IH G’ has no cycle. Hence G has no cycle.

  9. connected graph with no cycle connected graph with |V|-1 edges graph with |V|-1 edges and no cycles  Assume |V|-1 edges and no cycles. Let |G1|,...,|Gk| be the connected components. Then |E_i| = |V_i| - 1, hence |E| = |V| - k. Thus k = 1.

  10. Spanning trees

  11. Spanning trees

  12. Spanning trees

  13. Spanning trees How many spanning trees ?

  14. Spanning trees How many spanning trees ? 4

  15. Spanning trees How many spanning trees ?

  16. Spanning trees How many spanning trees ? 8

  17. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  18. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  19. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  20. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  21. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  22. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  23. Minimum weight spanning trees • Kruskal’s algorithm • sort the edges by weight • add edges in order • if they do not create cycle

  24. Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle K = MST output by Kruskal T = optimal MST Is K = T ?

  25. Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle K = MST output by Kruskal T = optimal MST Is K = T ? no – e.g. if all edge-weights are the same  many optima

  26. Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle K = MST output by Kruskal T = optimal MST Assume all edge weights are different. Then K=T. (In particular, unique optimum)

  27. Kruskal’s algorithm 1) sort the edges by weight 2) add edges in order if they do not create cycle K = MST output by Kruskal T = optimal MST G connected, e in a cycle  G-e connected

  28. Kruskal’s algorithm K = MST output by Kruskal T = optimal MST G connected, e in a cycle  G-e connected e the edge of the smallest weight in K-T. Consider T+e.

  29. Kruskal’s algorithm e the edge of the smallest weight in K-T. Consider T+e. Case 1: all edgeweights in C smaller that we Case 2: one edgeweight in C larger that we

  30. Kruskal’s algorithm • sort the edges by weight • add edges in order • if they do not create cycle Need to maintain components. Find-Set(u) Union(u,v)

  31. Union-Find S[1..n] for i  1 to n do S[i] i Find-Set(u) return S[u] Union(u,v) a  S[u] for i 1 to n do if S[i]=a then S[i]  S[v]

  32. Union-Find S[1..n] for i  1 to n do S[i] i Find-Set(u) return S[u] Union(u,v) a  S[u] for i 1 to n do if S[i]=a then S[i]  S[v] O(1) O(n)

  33. Kruskal’s algorithm O(1) Find-Set(u) Union(u,v) O(n) • Kruskal’s algorithm • sort the edges by weight • add edges in order • if they do not create cycle

  34. Kruskal’s algorithm O(1) Find-Set(u) Union(u,v) O(n) O(E log E + V^2) • Kruskal’s algorithm • sort the edges by weight • add edges in order • if they do not create cycle

  35. Union-Find 2 S[1..n] for i  1 to n do S[i] i n=|V| Find-Set(u) while (S[u] u) do u S[u] S[u] Union(u,v) S[Find-Set(u)] Find-Set(v) v u

  36. Union-Find 2 S[1..n] for i  1 to n do S[i] i n=|V| Find-Set(u) while (S[u] u) do u S[u] S[u] Union(u,v) S[Find-Set(u)] Find-Set(v) v u

  37. Union-Find 2 S[1..n] for i  1 to n do S[i] i n=|V| Find-Set(u) while (S[u] u) do u S[u] S[u] Union(u,v) S[Find-Set(u)] Find-Set(v) O(n) O(n)

  38. Union-Find 2 S[1..n] for i  1 to n do S[i] i n=|V| Find-Set(u) while (S[u] u) do u S[u] S[u] Union(u,v)u Find-Set(u); v Find-Set(v); if D[u]<D[v] then S[u] v if D[u]>D[v] then S[v] u if D[u]=D[v] then S[u]  v; D[v]++ O(log n) O(log n)

  39. Kruskal’s algorithm O(log n) Find-Set(u) Union(u,v) O(log n) • Kruskal’s algorithm • sort the edges by weight • add edges in order • if they do not create cycle

  40. Kruskal’s algorithm O(log n) Find-Set(u) Union(u,v) O(log n) O(E log E + (E+V)log V) • Kruskal’s algorithm • sort the edges by weight • add edges in order • if they do not create cycle

  41. Kruskal’s algorithm log E  log V2 = 2 log V = O(log V) O((E+V) log V) O(E log E + (E+V)log V) • Kruskal’s algorithm • sort the edges by weight • add edges in order • if they do not create cycle

  42. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  43. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  44. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  45. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  46. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  47. Minimum weight spanning trees 4 3 2 3 5 7 1 4 6 6 2

  48. Minimum weight spanning trees Prim’s algorithm 1) S  {1} 2) add the cheapest edge {u,v} such that uS and vSC S S{v} (until S=V)

  49. Minimum weight spanning trees 1) S  {1} 2) add the cheapest edge {u,v} such that uS and vSC S S{v} (until S=V) P = MST output by Prim T = optimal MST Is P = T ? assume all the edgeweights different

  50. Minimum weight spanning trees P = MST output by Prim T = optimal MST P = T assuming all the edgeweights different v1,v2,...,vn order added to S by Prim smallest i such that an edge e E connecting S={v1,...,vi} to SC different in T than in Prim (f)

More Related