1 / 4

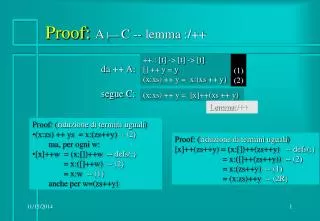
Proof: A | C -- lemma :/++

Proof: A | C -- lemma :/++. ++:: [t] -> [t] -> [t] [] ++ y = y (x:xs) ++ y = x:(xs ++ y). (1) (2). da ++ A:. segue C:. (x:xs) ++ y = [x]++(xs ++ y). Lemma:/++. Proof: ( riduzione di termini uguali ) (x:zs) ++ ys = x:(zs++y) -- (2) ma, per ogni w:

emerald-bryant
Télécharger la présentation

Proof: A | C -- lemma :/++

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Proof: A| C -- lemma :/++ ++:: [t] -> [t] -> [t] [] ++ y = y (x:xs) ++ y = x:(xs ++ y) (1) (2) da ++ A: segue C: (x:xs) ++ y = [x]++(xs ++ y) Lemma:/++ • Proof: (riduzione di termini uguali) • (x:zs) ++ ys = x:(zs++y) -- (2) ma, per ogni w: • [x]++w = (x:[])++w -- defs(:) • = x:([]++w) -- (2) • = x:w -- (1) • anche per w=(zs++y) Proof: (riduzione di termini uguali) [x]++(zs++y) = (x:[])++(zs++y) -- defs(:) = x:([]++(zs++y)) -- (2) = x:(zs++y) -- (1) = (x:zs)++y -- (2R)

  2. Proof: A| C -- reverse 1 reverse:: [t] -> [t] reverse [] = [] reverse (x:xs) = reverse xs ++ [x] (1) (2) da A: segue Cxs,ys: reverse (xs ++ ys) = (reverse ys) ++ (reverse xs) Proof: (Induzione sulla size delle liste) base: |xs|=0 => xs=[] & xs++ys = ys => reverse ([]++ys) = reverse ys ++ reverse[] |xs|=1 => xs=[x] => reverse([x]++ys) = reverse(x:[]++ys) = reverse(x:ys) -- defs(:) = reverse ys ++ [x] ---(2) = reverse ys ++ reverse [x] ---lemma rev[] generale: ind.hyp  k: xs: |xs|<k => Cxs,ys Sia xs: |xs| = k>1 => xs = x:zs per |zs|<k => => reverse(xs ++ ys) = reverse(x:zs ++ ys) = reverse([x] ++ (zs ++ ys)) ---lemma :/++ = reverse(zs ++ ys) ++ (reverse [x]) ---ind.hyp = (reverse ys) ++ (reverse zs) ++ (reverse [x]) ---ind.hyp = (reverse ys) ++ ((reverse zs) ++ (reverse [x])) ---ass++ = (reverse ys) ++ (reverse ([x]++zs)) ---ind.hyp = (reverse ys) ++ (reverse xs)

  3. Proof: A| C--- reverse 2 reverse:: [t] -> [t] reverse [] = [] reverse (x:xs) = reverse xs ++ [x] (1) (2) da A: segue Cxs,ys: reverse (xs ++ ys) = (reverse ys) ++ (reverse xs) Proof: (Induzione sulla size delle liste) base: |xs|+|ys|=0 => xs=[]=ys & xs++ys=[] => reverse [] = reverse [] ++ reverse[] generale: induc-hyp:  k: xs,ys: |xs|+|ys|<k => Cxs,ys Sia xs, ys: |xs|+|ys|=k>0 & |xs|≠0≠|ys| => xs = x:zs per |zs|+|ys|<k => => reverse(xs ++ ys) = reverse(x:zs ++ ys) = reverse(x:(zs ++ ys)) --- def(++(2)) = reverse(zs ++ ys) ++ [x] --- (2) = ((reverse ys) ++ (reverse zs)) ++ [x] ---ind.hyp. |zs|+|ys|<k = (reverse ys) ++ ((reverse zs) ++ [x]) --- lemma ass.++ = (reverse ys) ++ (reverse x:zs) ---(2R) = (reverse ys) ++ (reverse xs) Quando |xs|≠0&|ys|=0 ?

  4. Proof: lemmi [] ++ ys = ys (x:xs) ++ ys = x:(xs++ys) reverse [] = [] reverse (x:xs) = reverse xs ++ [x] da A: segue: lemma ass.++ (xs ++ ys) ++ zs = xs ++ (ys++zs) lemma rev[] reverse[x] = [x]

More Related