1 / 1

Optimizing Acoustic Horn Shapes to Minimize Reflection Using Fixed Mesh Methods

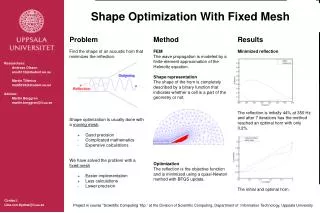
This study addresses the shape optimization of acoustic horns to minimize reflection using a fixed mesh approach. Traditional shape optimization relies on a moving mesh for precision but is hindered by complex mathematics and costly calculations. We implemented a shape representation through a binary function to define horn geometry and modeled wave propagation with finite-element approximation of the Helmholtz equation. Utilizing a quasi-Newton method with BFGS updates, our optimization achieved a remarkable reduction in reflection from 44% at 350 Hz to only 0.2% after 7 iterations.

etan
Télécharger la présentation

Optimizing Acoustic Horn Shapes to Minimize Reflection Using Fixed Mesh Methods

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Problem Find the shape of an acoustic horn that minimizes the reflection. Shape optimization is usually done with a moving mesh. + Good precision - Complicated mathematics - Expensive calculations We have solved the problem with a fixed mesh + Easier implementation + Less calculations - Lower precision Method FEM The wave propagation is modeled by a finite-element approximation of the Helmoltz equation. Shape representation The shape of the horn is completely described by a binary function that indicates whether a cell is a part of the geometry or not. Optimization The reflection is the objective function and is minimized using a quasi-Newton method with BFGS update. Results Minimized reflection The reflection is initially 44% at 350 Hz and after 7 iterations has the method reached an optimal horn with only 0.2%. The initial and optimal horn. Researchers: Andreas Olsson anol5113@student.uu.se Martin Tillenius mati5023@student.uu.se Advisor: Martin Berggren martin.berggren@it.uu.se Shape Optimization With Fixed Mesh Contact: Lina.von.Sydow@it.uu.se Project in course ”Scientific Computing 10p.” at the Division of Scientific Computing, Department of Information Technology, Uppsala University

More Related