Lecture 13: Associative Memory
900 likes | 1.28k Vues
Lecture 13: Associative Memory. References: D Amit, N Brunel, Cerebral Cortex 7 , 237-252 (1997) N Brunel, Network 11 , 261-280 (2000) N Brunel, Cerebral Cortex 13 , 1151-1161 (2003)

Lecture 13: Associative Memory
E N D
Presentation Transcript
Lecture 13: Associative Memory References: D Amit, N Brunel, Cerebral Cortex7, 237-252 (1997) N Brunel, Network11, 261-280 (2000) N Brunel, Cerebral Cortex13, 1151-1161 (2003) J Hertz, in Models of Neural NetworksIV (L van Hemmen, J Cowan and E Domany, eds) Springer Verlag, 2002; sect 1.4
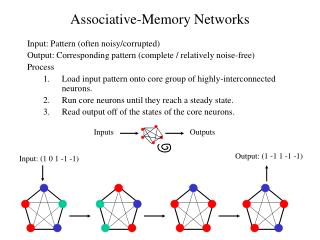
What is associative memory? • “Patterns”: firing activity of specific sets of neurons (Hebb: “assemblies”)
What is associative memory? • “Patterns”: firing activity of specific sets of neurons (Hebb: “assemblies”) • “Store” patterns in synaptic strengths
What is associative memory? • “Patterns”: firing activity of specific sets of neurons (Hebb: “assemblies”) • “Store” patterns in synaptic strengths • Recall: Given input (initial activity pattern) not equal to any stored pattern, network dynamics should take it to “nearest” (most similar) stored pattern
What is associative memory? • “Patterns”: firing activity of specific sets of neurons (Hebb: “assemblies”) • “Store” patterns in synaptic strengths • Recall: Given input (initial activity pattern) not equal to any stored pattern, network dynamics should take it to “nearest” (most similar) stored pattern (categorization, error correction, …)
Implementation in balanced excitatory-inhibitory network Model (Amit & Brunel): pnon-overlapping excitatory subpopulations
Implementation in balanced excitatory-inhibitory network Model (Amit & Brunel): pnon-overlapping excitatory subpopulations each of size n = fN (fp < 1)
Implementation in balanced excitatory-inhibitory network Model (Amit & Brunel): pnon-overlapping excitatory subpopulations each of size n = fN (fp < 1) stronger connections within subpopulations (“assemblies”)
Implementation in balanced excitatory-inhibitory network Model (Amit & Brunel): pnon-overlapping excitatory subpopulations each of size n = fN (fp < 1) stronger connections within subpopulations (“assemblies”) weakened connections between subpopulations
Implementation in balanced excitatory-inhibitory network Model (Amit & Brunel): pnon-overlapping excitatory subpopulations each of size n = fN (fp < 1) stronger connections within subpopulations (“assemblies”) weakened connections between subpopulations Looking for selective states: higher rates in a single assembly
Model Like Amit-Brunel model (Lecture 9) except for exc-exc synapses:
Model Like Amit-Brunel model (Lecture 9) except for exc-exc synapses: From within the same assembly:
Model Like Amit-Brunel model (Lecture 9) except for exc-exc synapses: From within the same assembly:
Model Like Amit-Brunel model (Lecture 9) except for exc-exc synapses: From within the same assembly: (strengthened, “Hebb” rule)
Model Like Amit-Brunel model (Lecture 9) except for exc-exc synapses: From within the same assembly: From outside the assembly: (strengthened, “Hebb” rule) (weakened, “anti-Hebb”)
Model Like Amit-Brunel model (Lecture 9) except for exc-exc synapses: From within the same assembly: From outside the assembly: Otherwise: no change (strengthened, “Hebb” rule) (weakened, “anti-Hebb”)
Model Like Amit-Brunel model (Lecture 9) except for exc-exc synapses: From within the same assembly: From outside the assembly: Otherwise: no change (strengthened, “Hebb” rule) (weakened, “anti-Hebb”) To conserve average strength:
Model Like Amit-Brunel model (Lecture 9) except for exc-exc synapses: From within the same assembly: From outside the assembly: Otherwise: no change (strengthened, “Hebb” rule) (weakened, “anti-Hebb”) To conserve average strength: =>
Mean field theory Rates: active assembly inactive assemblies rest of excitatory neurons inhibitory neurons ext input neurons
Mean field theory Rates: active assembly inactive assemblies rest of excitatory neurons inhibitory neurons ext input neurons Input current to neurons in the active assembly:
Mean field theory Rates: active assembly inactive assemblies rest of excitatory neurons inhibitory neurons ext input neurons Input current to neurons in the active assembly: to rest of assemblies:
Mean field theory Rates: active assembly inactive assemblies rest of excitatory neurons inhibitory neurons ext input neurons Input current to neurons in the active assembly: to rest of assemblies: to other excitatory neurons:
Mean field theory Rates: active assembly inactive assemblies rest of excitatory neurons inhibitory neurons ext input neurons Input current to neurons in the active assembly: to rest of assemblies: to other excitatory neurons: to inhibitory neurons:
Mean field theory (2) Noise variances (white noise approximation):
Mean field theory (2) Noise variances (white noise approximation):
Mean field theory (2) Noise variances (white noise approximation):
Mean field theory (2) Noise variances (white noise approximation):
Mean field theory (2) Noise variances (white noise approximation):
Mean field theory (2) Noise variances (white noise approximation): Rate of an I&F neuron driven by white noise:
Mean field theory (2) Noise variances (white noise approximation): Rate of an I&F neuron driven by white noise:
Spontaneous activity: All assemblies inactive:
Spontaneous activity: All assemblies inactive:
Spontaneous activity: All assemblies inactive: becomes
Spontaneous activity: All assemblies inactive: becomes Similarly,
Spontaneous activity: All assemblies inactive: becomes Similarly,
Spontaneous activity: All assemblies inactive: becomes Similarly, and
Spontaneous activity: All assemblies inactive: becomes Similarly, and
Spontaneous activity: All assemblies inactive: becomes Similarly, and Solve for
Simplified model (Brunel 2000) • pf << 1
Simplified model (Brunel 2000) • pf << 1 • g+ ~1/f >> 1
Simplified model (Brunel 2000) • pf << 1 • g+ ~1/f >> 1 • variances s+ = sact, s1 as in spontaneous-activity state
Simplified model (Brunel 2000) • pf << 1 • g+ ~1/f >> 1 • variances s+ = sact, s1 as in spontaneous-activity state Define L = fJ11g+
Simplified model (Brunel 2000) • pf << 1 • g+ ~1/f >> 1 • variances s+ = sact, s1 as in spontaneous-activity state Define L = fJ11g+ Then (1) spontaneous activity state has r+= r1,
Simplified model (Brunel 2000) • pf << 1 • g+ ~1/f >> 1 • variances s+ = sact, s1 as in spontaneous-activity state Define L = fJ11g+ Then (1) spontaneous activity state has r+= r1, (2) In recall state with ract > r+, r1 andr2 are same as in spontaneous activity state
Simplified model (Brunel 2000) • pf << 1 • g+ ~1/f >> 1 • variances s+ = sact, s1 as in spontaneous-activity state Define L = fJ11g+ Then (1) spontaneous activity state has r+= r1, (2) In recall state with ract > r+, r1 andr2 are same as in spontaneous activity state (3) ract is determined by
Graphical solution (r -> n) (This L = (our L) x tm)
Graphical solution (r -> n) (This L = (our L) x tm) 1-assembly memory/recall state stable for big enough L (or g+ ) ~ describes “working memory” in prefrontal cortex
Capacity problem In this model, memory assemblies were non-overlapping. This is unrealistic.