1 / 8

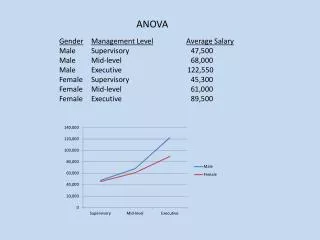
ANOVA

ANOVA. One Way Analysis of Variance. ANOVA. Purpose: To assess whether there are differences between means of multiple groups. ANOVA provides evidence. We compare variation among the means of the groups with the variation within groups. Hence the name Analysis of Variance. ANOVA HYPOTHESES.

flynn
Télécharger la présentation

ANOVA

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. ANOVA One Way Analysis of Variance

  2. ANOVA • Purpose: To assess whether there are differences between means of multiple groups. ANOVA provides evidence. • We compare variation among the means of the groups with the variation within groups. • Hence the name Analysis of Variance

  3. ANOVA HYPOTHESES • Tests the null hypothesis that the population means are all equal. • Ho: μ1 = μ2 = μ3 = μ4 = μ5 • Ha: not all of the μi are equal.

  4. ANOVA ASSUMPTIONS • The populations are normally distributed. • The standard deviations of the populations are equal. • Moore and McCabe p. 755: • Rule for examining standard deviation in ANOVA • If the largest standard deviation is less than twice the smallest standard deviation, we can use methods based on the assumption of equal standard deviations and our results will be approximately correct.

  5. Pooled Estimator of σ • When we assume that the population standard deviations are equal, each sample standard deviation is an estimate of σ. • To combine into a single estimate use pooled sample variance. • Sp = Root Mean Square Error (Root MSE)

  6. ANOVA TABLE • Sum of Squares—represents variation in data, a sum of squared deviations SSTotal = SSGroups + SSError • SST - Measures variation around the overall mean • SSG-Variation of the groups means around the overall means • SSE-measures variation of each observation around its group mean.

  7. ANOVA Table Continued • Degrees of Freedom • Degrees of Freedom Total = N – 1 • Degrees of Freedom Group = I – 1 • Degrees of Freedom Error = N – I • (I = number of groups) • DFT = DFG + DFE • Sp2 = MSE = SSE/DFE • MSG = SSG/DFG

  8. F-Statistic • If use ANOVA to compare 2 populations, the F-Statistic is exactly equal to the square of the t-statistic. • F statistic = MSG/MSE • Use Notation F (I-1, N-I)

More Related