1 / 37

Understanding Neuroticism and IQ Scores: Statistical Insights and Calculations

This guide explores the calculations of neuroticism scores and IQ thresholds based on z-scores. It illustrates how to determine the likelihood of individuals scoring within specific ranges using standard deviations and mean values. Practical examples include finding the IQ score needed to be in the top 20% and the bottom 10% of the population, as well as determining scores for academic acceptance. It provides a step-by-step approach to statistical problem-solving relevant to psychological assessments and their real-world applications.

galvin
Télécharger la présentation

Understanding Neuroticism and IQ Scores: Statistical Insights and Calculations

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

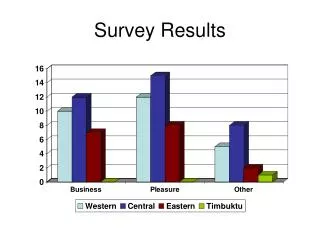
  1. Survey Results

  2. Practice • The Neuroticism Measure = 23.32 S = 6.24 n = 54 How many people likely have a neuroticism score between 29 and 34?

  3. Practice • (29-23.32) /6.24 = .91 • B = .3186 • ( 34-23.32)/6.26 = 1.71 • B =.4564 • .4564-.3186 = .1378 • .1378*54 = 7.44 or 7 people

  4. Finding a score when given a probability • What IQ score is required to fall in the top 20 percent of the population?

  5. Step 1: Sketch out question .20 100 ?

  6. Step 2: Look in Table C In column C get as close to .20 as you can and find the corresponding Z score = .84 .20 100 ?

  7. Step 3: Find the X score that goes with the Z score • Z score = .84 • Z = (X -  ) /  • .84 = (X - 100) / 15 • Must solve for X • X =  + (z)() • X = 100 + (.84)(15)

  8. Step 3: Find the X score that goes with the Z score • Z score = .84 • Z = (X -  ) /  • .84 = (X - 100) / 15 • Must solve for X • X =  + (z)() • X = 100 + (.84)(15) = 112.6 • A score of 112.6 is needed to be in the top 20 percent!

  9. Finding a score when given a probability • What IQ score is required to fall in the bottom 10 percent of the population?

  10. Step 1: Sketch out question .10 100

  11. Step 2: Look in Table C In column C get as close to .10 as you can and find the corresponding Z score = - 1.28 (NOTICE-NEGATIVE) .10 100

  12. Step 3: Find the X score that goes with the Z score • Must solve for X • X =  + (z)() • 80.8 = 100 + (-1.28)(15)

  13. Step 3: Find the X score that goes with the Z score • Must solve for X • X =  + (z)() • 80.8 = 100 + (-1.28)(15) • Thus, a you need an IQ of 80.8 to fall in the bottom 10 percent of the population

  14. Practice • On the next test I will give an A to the top 5 percent of this class. • The average test grade is 56.82 with a SD of 6.98. • How many points on the test did you need to get to get an A?

  15. Step 1: Sketch out question .05

  16. Step 2: Look in Table C In column C get as close to .05 as you can and find the corresponding Z score = 1.64 .05

  17. Step 3: Find the X score that goes with the Z score • Must solve for X • X =  + (z)() • 68.26 = 56.82 + (1.64)(6.98)

  18. Step 3: Find the X score that goes with the Z score • Must solve for X • X =  + (z)() • 68.26 = 56.82 + (1.64)(6.98) • Thus, a you need a score of 68.26 to get an A

  19. Practice • The prestigious Whatsamatta U will only take people scoring in the top 97% on the verbal section SAT (i.e., they reject the bottom 3%). • What is the lowest score you can get on the SAT and still get accepted? • Mean = 500; SD = 100

  20. Step 1: Sketch out question .03

  21. Step 2: Look in Table C In column C get as close to .03 as you can and find the corresponding Z score = -1.88 .03

  22. Step 3: Find the X score that goes with the Z score • Must solve for X • X =  + (z)() • 312 = 500 + (-1.88)(100)

  23. Step 3: Find the X score that goes with the Z score • Must solve for X • X =  + (z)() • 312 = 500 + (-1.88)(100) • Thus, you need a score of 312 on the verbal SAT to get into this school

  24. Practice • IQ Tests • Mean = 100 • SD = 15 • 7.11 • 7.12

  25. 7.11 Z = -2.0 p = .0228 • 7.12 (.0228)(4000) = 91.2 students

  26. Practice • IQ Tests • Mean = 100 • SD = 15 • 7.15 • 7.16

  27. 7.15 p =.02; Z = 2.06 100 + (2.06)(15) = 130.9 • 7.16 a) p = .05; Z = 1.65 (1.64 is fine too) 64.3 + (1.65)(2.5) = 68.4 inches b) (58 – 64.3)/2.5 = -2.52 p = .0059

  28. Practice • Page 136 • 7.19 • 7.21

  29. 7.19 a) Z = (30-35)/6 = -.83; p = .2967 Z = (40-35)/6 = .84; p =.2967 p = .2967 + .2967 = .5934 b) .5934 • 7.21 Z = (20-35)/6 = -2.50; p = .4938 Z = (30-35)/6 = -.83; p =.2967 p = .4938 - .2067 = .1971

  30. Practice • 6.22

  31. Practice • X = Stanford-Binet • Y = WAIS • b = .80 (15 / 16) = .75 • a = 100 – (.75)100 = 25 • Y = 25 + (.75)X • 73.75 = 25 + (.75)65 • It’s a bad idea to use the same cut off score for these two tests

  32. Practice • 6.5

  33. Practice • Page 96 # 5.5 • r = .51

  34. Practice • 7.27 • 7.29

More Related