Ch. 5b Linear Models & Matrix Algebra
430 likes | 999 Vues
Ch. 5b Linear Models & Matrix Algebra. 5.5 Cramer's Rule 5.6 Application to Market and National-Income Models 5.7 Leontief Input-Output Models 5.8 Limitations of Static Analysis. 5.2 Evaluating a third-order determinant Evaluating a 3rd order determinant by Laplace expansion.

Ch. 5b Linear Models & Matrix Algebra
E N D
Presentation Transcript
Ch. 5b Linear Models & Matrix Algebra 5.5 Cramer's Rule 5.6 Application to Market and National-Income Models 5.7 Leontief Input-Output Models 5.8 Limitations of Static Analysis
5.2 Evaluating a third-order determinantEvaluating a 3rd order determinant by Laplace expansion Ch. 5a Linear Models and Matrix Algebra 5.1 - 5.4
5.5 Deriving Cramer’s Rule (nxn) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.5 Deriving Cramer’s Rule (3x3) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.5 Deriving Cramer’s Rule (3x3) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.5 Deriving Cramer’s Rule (3x3) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.5 Deriving Cramer’s Rule (3x3) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.5 Deriving Cramer’s Rule (nxn) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.5 Deriving Cramer’s Rule (nxn) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.5 Deriving Cramer’s Rule (nxn) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.6 Applications to Market and National-income Models: Matrix Inversions Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.6 Macro model • Section 3.5, Exercise 3.5-2 (a-d), p. 47 and • Section 5.6, Exercise 5.6-2 (a-b), p. 111 • Given the following model (a) Identify the endogenous variables (b) Give the economic meaning of the parameter g (c) Find the equilibrium national income (substitution) (d) What restriction on the parameters is needed for a solution to exist? Find Y, C, G by (a) matrix inversion (b) Cramer’s rule Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.6 The macro model (3.5-2, p. 47) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.6 The macro model (3.5-2, p. 47) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.6 Application to Market & National Income Models: Cramer’s rule (3.5-2, p. 47) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.6 Application to Market & National Income Models: Matrix Inversion (3.5-2, p. 47) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.6 Application to Market & National Income Models: Matrix Inversion (3.5-2, p. 47) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Miller and Blair 2-3, Table 2-3, p 15 Economic Flows ($ millions) Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Miller and Blair 2-3, Table 2-3, p 15 Inter-industry flows as factor shares Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Miller & Blair, p. 102 Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.7 Leontief Input-Output Models Structure of an input-output model Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
5.8 Limitations of Static Analysis • Static analysis solves for the endogenous variables for one equilibrium • Comparative statics show the shifts between equilibriums • Dynamics analysis looks at the attainability and stability of the equilibrium Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8
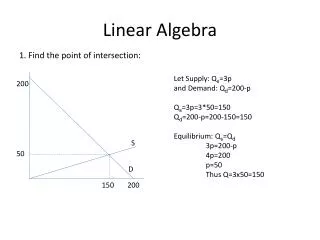
5.6 Application to Market and National-Income Models Market model National-income model Matrix algebra vs. elimination of variables • Why use matrix method at all? • Compact notation • Test existence of a unique solution • Handy solution expressions subject to manipulation Ch. 5b Linear Models and Matrix Algebra 5.5 - 5.8