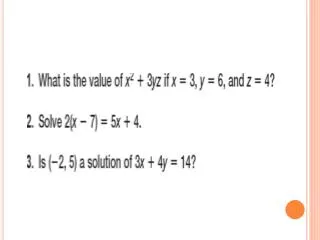1.3 Measuring Segments
250 likes | 537 Vues
1.3 Measuring Segments. Objectives -learn symbols for rays and segments -Define Postulate -Identify Ruler Postulate -Identify Segment Addition Postulate. T. V. M. -2. -1. 0. 1. 2. 3.

1.3 Measuring Segments
E N D
Presentation Transcript
1.3 Measuring Segments Objectives -learn symbols for rays and segments -Define Postulate -Identify Ruler Postulate -Identify Segment Addition Postulate
T V M -2 -1 0 1 2 3 On a number line, every point is paired with a number and every number paired with a point. It is often necessary to know the length of a segment on a number line. In this case we want to know the length of MV, which we denote just MV. Without the symbol above the 2 points it is showing us that we are talking about length.
To find the length of a segment on a number line, you simply subtract the two endpoints values and then take the absolute value.
Postulates (or Axioms) these are statements that we have to assume true because we can not prove them. • REMEMBER POSTULATES BY THEIR STATEMENT • A Little Bit of History • The geometry that we are most familiar with is called Euclidian Geometry named after the mathematician Euclid who realized/discovered/defined 5 (some argue 6) basic undeniable rules in which set the foundation for all other rules in geometry. Without Euclid’s 5 absolute truths (axioms) we would not have geometry. Authors of today’s textbooks have divided his axioms up so that they are easier to deal with. We will be referring to them as postulates.
Ruler Postulate The distance between points A and B is the absolute value of the difference of their coordinates, or |a-b|. This value would be referred to as AB.
Example. • B is between A and C, with AB=x, BC=x+6, and AC =24. • FIND the value of x, and BC.
In geometry when 2 or more objects have the same size and shape, they are said to be congruent. • Congruent segments segments that have equal lengths. 8 cm 8 cm Z M T A Difference between Equality and Congruency. Equality is when numerical expressions have the same value then the expressions are said to be equal. When two segments have the same length they are said to be congruent.
To show that that AM and TZ have equal lengths you write: To show that AM and TZ are congruent, you write 8 cm 8 cm Z M T A
Midpoint the point that divides the segment into 2 congruent segments. • Bisector of a segment a line, segment, ray, or plane that intersects the segment at its midpoint. • So it is any geometric figure that cuts a segment into 2 congruent parts.
Homework • Section 1.3 found on MathXLforSchool.com