Computer Graphics Conceptual Model
390 likes | 935 Vues
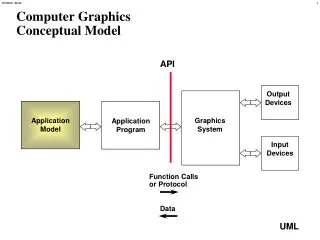
Computer Graphics Conceptual Model API Output Devices Application Model Graphics System Application Program Input Devices Function Calls or Protocol Data Modeling in Three Dimensions Two Approaches Constructive Solid Geometry (CSG)

Computer Graphics Conceptual Model
E N D
Presentation Transcript
Computer GraphicsConceptual Model API Output Devices Application Model Graphics System Application Program Input Devices Function Calls or Protocol Data
Modeling in Three DimensionsTwo Approaches • Constructive Solid Geometry (CSG) • Primitives are a small set of volumetric objects such as cube, pyramid, sphere, etc. • Objects built from normalized set operations on these objects • Boundary (surface) representation • Objects are described by their surfaces and can be thought of as being hollow • Surfaces composed (approximated) by simple, convex, planar polygons • Objects can be specified through a set of vertices in three dimensions • Implies underlying coordinate system • Duality: Object <--> Object representation
0 A 3 B 2 C 1 D E F Representation of a CubeSurface Representation Data Structure VERTEX LISTS FACES VERTICES 5 6 X0, Y0, Z0 X1, Y1, Z1 1 X2, Y2 , Z2 2 X3, Y3 , Z3 4 7 X4, Y4 , Z4 3 X5, Y5 , Z5 7 0 3 X6, Y6 , Z6 6 X7, Y7 , Z7 2 Representation: data structure . . . Object: set of points
Inward and Outward Pointing Faces:Right Hand Rule Outside 3 2 0 1
Transformations • Maps an object into another object • In general, a transformation maps every point on an object to another point in the underlying coordinate space. • Why do we want/need transformations? • Change size, location, orientation of objects without changing underlying model (or primitive drawing commands) • Animation • Instancing Transformation Object New Object Representation New Representation Operation
P1’ P2’ What Do We Require of Transforms?Line Preserving P1 Line Not Preserved P2
Abstract Data Types:Affine Space • Scalar a, b, d, e • Magnitude (e.g. real numbers) • Vector u, v, w, x • Direction • Magnitude • No Position • Point P, Q, R, X • Position • No Direction • No Magnitude
Defined Operations:Scalars • Addition: a+b • Additive identity: zero • Additive inverse: - b • Subtraction defined in terms of additive inverse • Multiplication: d * j • Multiplicative identity: 1 • Multiplicative inverse: 1/ d • Division defined in terms of multiplicative inverse
u q v Defined Operations:Vectors Dot Product Cross Product Addition v u u + v q v u Produces vector w orthogonal to u and v. u · v = | u | | v | cos q Magnitude (produces scalar) | u | = b w = u x v | w | = | u | | v | sin q (produces scalar)
Defined Operations:Scalars and Vectors Multiplication of vector by scalar: Produces vector u v = a u |a u | = a | u |
Defined Operations:Points and Vectors Affine Addition: Point + Vector = Point Q v P Q = P + v Related to point subtraction.
Defined Operations:Points Subtraction (Addition of points has no meaning.) P u = P - R R Produces vector
Lines in Affine Space R’ R Q v Q = P + v P R = P + a v - ¥ < a < ¥ Line segment from P to Q defined when: 0 £ a £ 1
Planes in Affine Space Planes are defined uniquely by three points: P, Q, R W(l) Q u = Q - P v = R - P u T( b) R P v S(a) S(a) = P + a v T(b) = P + b u W(a, b, l) = S +l (T - S) = P + a v + l (b u - a v) W (a, b, l) = P + a ( 1 - l ) v + l b u W = P + d v + c u
Representations of Points and Vectors Coordinate system: y P (x, y, z) v x z where:
Homogeneous Coordinates Frame is specified by: where are linearly independent basis vectors and P0 arbitrary point Frame Homogeneous coordinate representation:
Affine AdditionIn Homogeneous Coordinate Representation Point Point Scalar times vector
y x Transform as aChange of Frame y’ Want to translate by:Dx = 2, Dy=4 (2, 3) in x’y’ (4,7) in x y y x’ (2, 3) Dx = 2, Dy=4 x 1. Transform frame 2. Find representation in original frame
Transform as aChange of Frame Representation: Frame:
Transformation Matrix Original Frame: Transformed Frame: Express elements of transformed frame in original frame: where:
is representation in transformed frame is representation in original frame Transformation of Representation where is of the form:
Affine Transformations T(point) -> point T(vector) -> vector
P1’ P2’ What Do We Require of Transforms?Line Preserving P1 Line Not Preserved P2
Affine Transformation:Line Preservation Matrix multiplication is linear. Therefore: T(p)+aT(v) p+av v T(v) p T(p) Meets our requirements!
Translation Assumptions: Translate the new frame:
Scaling Scale the new frame:
Rotation Rotation around the z axis: q
Rotation About x and y axes Similar derivations give:
Concatenation of Transformations Apply T1, Then apply T2:
OpenGL Matrix Operations glLoadIdentity(); Loads an identity matrix onto the top of the current stack glLoadMatrixf(pointer_to_matrix); Loads arbitrary matrix onto top of the current stack glMultMatrixf(pointer_to_matrix); Postmultiplies current matrix by arbitrary matrix Matricies are one-dimensional arrays of type GLfloat in column major order.
Predefined Postmultiplier Operatorsin OpenGL glTranslatef(dx, dy, dz); Multiplies current matrix with translation matrix. dx, dy, and dz are translations along x,y, and z axes. glRotatef(angle, x, y, z); Multiplies current matrix with rotation about the line from the origin through the point (x, y, z) by angle. Right hand rule applies. Angle in degrees. glScalef(sx, sy, sz); Multiplies current matrix with scaling matrix. sx, sy, sz are the scale factors along the x, y, and z axes.
Load Matrix Current Current Stack Stack Transformation Matrices in OpenGL Matrix Mode 3D Model Vertices 2D 3D Vertices Modelview Projection