1 / 37

Robust Feature-Based Alignment for Large-Scale Image Matching and Transformation

Robust feature-based alignment techniques are essential for accurately aligning images without pre-existing correspondences. The process involves extracting features, computing putative matches, hypothesizing transformations, and verifying these transformations by checking for consistency across other matches. Techniques such as SIFT feature descriptors enhance robustness to changes in illumination and small deformations. This method scales effectively for large databases, utilizing efficient putative match generation and approximate descriptor similarity searches, enabling the alignment of test images with extensive model databases.

kessie-garrett
Télécharger la présentation

Robust Feature-Based Alignment for Large-Scale Image Matching and Transformation

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

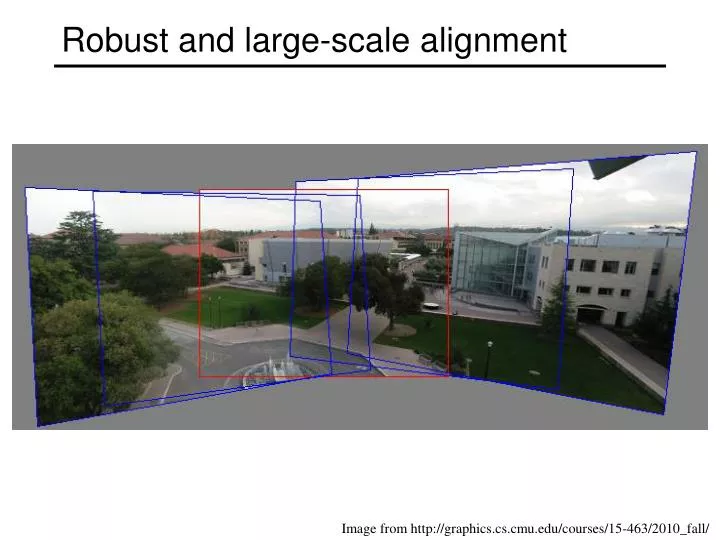
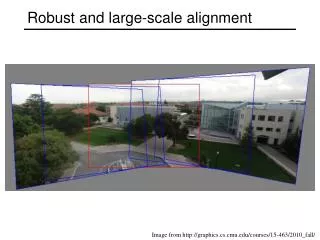
  1. Robust and large-scale alignment Image from http://graphics.cs.cmu.edu/courses/15-463/2010_fall/

  2. Robust feature-based alignment • So far, we’ve assumed that we are given a set of “ground-truth” correspondences between the two images we want to align • What if we don’t know the correspondences?

  3. Robust feature-based alignment • So far, we’ve assumed that we are given a set of “ground-truth” correspondences between the two images we want to align • What if we don’t know the correspondences? ?

  4. Robust feature-based alignment

  5. Robust feature-based alignment • Extract features

  6. Robust feature-based alignment • Extract features • Compute putative matches

  7. Robust feature-based alignment • Extract features • Compute putative matches • Loop: • Hypothesize transformation T

  8. Robust feature-based alignment • Extract features • Compute putative matches • Loop: • Hypothesize transformation T • Verify transformation (search for other matches consistent with T)

  9. Robust feature-based alignment • Extract features • Compute putative matches • Loop: • Hypothesize transformation T • Verify transformation (search for other matches consistent with T)

  10. Generating putative correspondences ?

  11. ( ) ( ) Generating putative correspondences • Need to compare feature descriptors of local patches surrounding interest points ? ? = featuredescriptor featuredescriptor

  12. Feature descriptors • Recall: covariant detectors => invariant descriptors Compute appearancedescriptors Detect regions Normalize regions

  13. Feature descriptors • Simplest descriptor: vector of raw intensity values • How to compare two such vectors? • Sum of squared differences (SSD) • Not invariant to intensity change • Normalized correlation • Invariant to affine intensity change

  14. Disadvantage of intensity vectors as descriptors • Small deformations can affect the matching score a lot

  15. Feature descriptors: SIFT • Descriptor computation: • Divide patch into 4x4 sub-patches • Compute histogram of gradient orientations (8 reference angles) inside each sub-patch • Resulting descriptor: 4x4x8 = 128 dimensions David G. Lowe. "Distinctive image features from scale-invariant keypoints.”IJCV 60 (2), pp. 91-110, 2004.

  16. Feature descriptors: SIFT • Descriptor computation: • Divide patch into 4x4 sub-patches • Compute histogram of gradient orientations (8 reference angles) inside each sub-patch • Resulting descriptor: 4x4x8 = 128 dimensions • Advantage over raw vectors of pixel values • Gradients less sensitive to illumination change • Pooling of gradients over the sub-patches achieves robustness to small shifts, but still preserves some spatial information David G. Lowe. "Distinctive image features from scale-invariant keypoints.”IJCV 60 (2), pp. 91-110, 2004.

  17. Feature matching • Generating putative matches: for each patch in one image, find a short list of patches in the other image that could match it based solely on appearance ?

  18. Feature space outlier rejection • How can we tell which putative matches are more reliable? • Heuristic: compare distance of nearest neighbor to that of second nearest neighbor • Ratio of closest distance to second-closest distance will be highfor features that are not distinctive • Threshold of 0.8 provides good separation David G. Lowe. "Distinctive image features from scale-invariant keypoints.”IJCV 60 (2), pp. 91-110, 2004.

  19. Reading David G. Lowe. "Distinctive image features from scale-invariant keypoints.”IJCV 60 (2), pp. 91-110, 2004.

  20. RANSAC • The set of putative matches contains a very high percentage of outliers • RANSAC loop: • Randomly select a seed group of matches • Compute transformation from seed group • Find inliers to this transformation • If the number of inliers is sufficiently large, re-compute least-squares estimate of transformation on all of the inliers • Keep the transformation with the largest number of inliers

  21. RANSAC example: Translation Putative matches

  22. RANSAC example: Translation Select one match, count inliers

  23. RANSAC example: Translation Select one match, count inliers

  24. RANSAC example: Translation Select translation with the most inliers

  25. Scalability: Alignment to large databases • What if we need to align a test image with thousands or millions of images in a model database? • Efficient putative match generation • Approximate descriptor similarity search, inverted indices Test image ? Model database

  26. Scalability: Alignment to large databases • What if we need to align a test image with thousands or millions of images in a model database? • Efficient putative match generation • Fast nearest neighbor search, inverted indexes Test image D. Nistér and H. Stewénius, Scalable Recognition with a Vocabulary Tree, CVPR 2006 Vocabulary tree with inverted index Database

  27. Descriptor space Slide credit: D. Nister

  28. Hierarchical partitioning of descriptor space (vocabulary tree) Slide credit: D. Nister

  29. Vocabulary tree/inverted index Slide credit: D. Nister

  30. Populating the vocabulary tree/inverted index Model images Slide credit: D. Nister

  31. Model images Populating the vocabulary tree/inverted index Slide credit: D. Nister

  32. Model images Populating the vocabulary tree/inverted index Slide credit: D. Nister

  33. Model images Populating the vocabulary tree/inverted index Slide credit: D. Nister

  34. Test image Model images Looking up a test image Slide credit: D. Nister

  35. Voting for geometric transformations • Modeling phase: For each model feature, record 2D location, scale, and orientation of model (relative to normalized feature coordinate frame) index model

  36. Voting for geometric transformations • Test phase: Each match between a test and model feature votes in a 4D Hough space (location, scale, orientation) with coarse bins • Hypotheses receiving some minimal amount of votes can be subjected to more detailed geometric verification index test image model

  37. Indexing with geometric invariants • When we don’t have feature descriptors, we can take n-tuples of neighboring features and compute invariant features from their geometric configurations • Application: searching the sky: http://www.astrometry.net/ B C D A

More Related