1 / 7

Mathematics of Dilations: Exploring Size Changes in Figures

A dilation is a transformation that changes the size of a figure but preserves its shape. In this exercise, Triangle ABC is graphed with an image using a scale factor of 2. The coordinates of the vertices A(0,0), B(4,0), C(0,5) are transformed according to the dilation rules. Explore if increasing the coordinates by 2 or multiplying them by 2 results in similar triangles. A hands-on application of dilations in geometry awaits!

larya
Télécharger la présentation

Mathematics of Dilations: Exploring Size Changes in Figures

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 2.4: Dilations CCSS

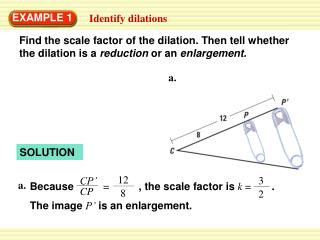
  2. A dilationis a transformation that changes the size of a figure but not its shape. The pre-image and the image are always similar shapes. A scale factorfor a dilation with a center at the origin is k, which is found by multiplying each coordinate by k: (a, b)  (ka, kb).

  3. Given Triangle ABC, graph the image Of ABC with a scale factor of 2. (2x, 2y) Image Pre-Image A (1,4) A ‘ (2,8) B (5,1) B ‘(10,2) C (0,0) C ‘ ( 0,0)

  4. Triangle ABC has vertices A ( 0,0) , B( 4,0) , C (0,5). Graph it • If the coordinates of each vertex of ABC are increased by 2, • will the new triangle be similar to triangle ABC (Graph it)? Why or why not? • 2) If the coordinates of each vertex of Triangle ABC are multiplied by 2, • will the new triangle be similar to Triangle ABC (Graph it)? Why or why not?

More Related