1 / 19

第四节 函数的单调性和曲线的凹凸性

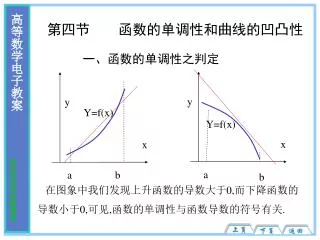
y. y. Y=f(x). Y=f(x). x. x. a. a. b. b. 第四节 函数的单调性和曲线的凹凸性. 一、函数的单调性之判定. 在图象中我们发现上升函数的导数大于 0, 而下降函数的 导数小于 0, 可见 , 函数的单调性与函数导数的符号有关. 定理 1 设函数 f(x) 在闭区间 [a,b] 上连续 , 在开区间 (a,b) 内可导 , 则 f(x) 在 [a,b] 上单调上升 ( 下降 ) 的 充分必要条件是在 (a,b) 内 f ’ (x) ≥0(≤0)

lorin
Télécharger la présentation

第四节 函数的单调性和曲线的凹凸性

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. y y Y=f(x) Y=f(x) x x a a b b 第四节 函数的单调性和曲线的凹凸性 一、函数的单调性之判定 在图象中我们发现上升函数的导数大于0,而下降函数的 导数小于0,可见,函数的单调性与函数导数的符号有关.

  2. 定理1设函数f(x)在闭区间[a,b]上连续,在开区间(a,b) 内可导,则f(x) 在[a,b]上单调上升(下降)的 充分必要条件是在(a,b)内f’(x)≥0(≤0) 即在[a,b]上f(x)单调上升→在(a,b)内f’(x)≥0; 在[a,b]上f(x)单调下降→在(a,b)内f’(x) ≤0;. 证明: 我们只证明单调上升的情况 必要性, 设在[a,b]上f(x)单调上升,任意取一点 x0∈(a,b),及x ∈[a,b], 不论x>x0还是x<x0,由于f(x) 单调上升,都有

  3. y Y=f(x) x a x x0 x b 又函数在(a,b)内可导,f’(x0)存 在,对它取极限得到 由x0的任意性,知必要性成立. 充分性. 设在(a,b)内f’(x)≥0,再设x1,x2是[a,b]内任意两点, 设x1<x2, 由中值定理,有 证明完毕

  4. 例1 讨论函数的单调性 推论:若函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,则 (1) 在(a,b)内f’(x)>0在→[a,b]上f(x)严格单调上升. (2) 在(a,b)内f’(x) <0 →在[a,b]上f(x)严格单调下降; 解: 当x=3,x=-1和x≠1,现在分四个区间讨论

  5. 区 间 y’ 函数的单调性 (-∞,-1] f’(x)≥0 单调上升 [-1,1) f’(x) ≤0单调下降 (1,3] f’(x) ≤0 单调下降 [3,+ ∞) f’(x)≥0 单调上升 3 -1 1 x

  6. y y x2 x2 x1 x x1 x 二 曲 线 的 凹 凸 性 与 拐 点 上面我们研究了函数单调性的判定方法,函数的单调性表示 曲线的上升和下降,图中的曲线是上升的,但它们的凹凸性不 同.在几何上,我们在曲线弧上任意两点的弦总是在弧的下面, 有的在弧的上方曲线的这种性质我们称为曲线的凹凸性.

  7. 我们称为向上凹的 如果恒有 我们称为向上凸的 定义 设f(x)在区间I上连续,如果对I上任意两点x1,x2.恒有 如果我们用二阶导数的符号来表示的话,我们有定理2

  8. 定理2设f(x)在[a,b]上连续,在(a,b)内具有一阶二阶导数,定理2设f(x)在[a,b]上连续,在(a,b)内具有一阶二阶导数, 那么: (1)若在(a,b)内f”(x)>0,则f(x)在[a,b]上的图形是凹的 (2)若在(a,b)内f”(x)<0,则f(x)在[a,b]上的图形是凸的. 证明: 在(1)的情况,设x1和x2是[a,b]内任意两点,且x1<x2, 记(x1+x2)/2=x0,并记 x2-x0=x0-x1=h, 则x1=x0-h, x2=x0+h 由拉格朗日中值公式,得到

  9. 所以是凹的

  10. y y x x y Y=lnx 是上凸的 解: x 解: 记忆方法 例1 讨论函数y=lnx(x>0)的凹凸性 例2 讨论函数y=sinx在其一个周期(0,2π)内的凹凸性 sinx在(0, π)内上凸,在(π,2 π)内上凹.

  11. y y=sinx x 二 拐 点 在y=sinx的曲线中,当x=π时, 其左邻域为上凸 (y”<0)右邻域为 下凹(y”>0).它是曲线的凹凸性的 分界点称为拐点 定义2 曲线f(x)的向上凸部分与向下凹部分的分解点称 为该曲线的拐点.

  12. 定理3 (必要条件) 若函数f(x)在(a,b)上二阶可导,则曲线 f(x)上的点 (x0,f(x0))为拐点的必要条件是f”(x0)=0 可能的拐点只有两种情况: (1)它是方程f”(x0)=0的根, (2)它f”(x)不存在的点,即函数f(x)的二阶不可导点. (判别 时看左右两边是否变号).

  13. 曲线是凹的 曲线是凸的 曲线是凹的 例3 求下列曲线的拐点 解: 则1，3可能是拐点

  14. y x y x x=1,x=3是曲线的拐点. 没有使y“(x)=0的点,但当x=0时y“不存在,点(0,0)可能是拐点. 当x<0时, y“>0,当x>0, y“<0, 即在x=0的左,右两边y“变号,表示它是拐点. 所以在两阶导数不存在时,需要用它的左右是否变号来 分析它的拐点. 

  15. y y=f(x) p y=kx+b N M Q x 三 渐 近 线 定义3 若曲线s上的动点p 沿着曲线无限地远离原点时,点 p与某一固定直线L之间的距离 趋近于0,则称直线L为曲线s的渐近线. 1， 斜渐近线 y=kx+b p是动点,它到直线L的距离

  16. L p α α N M 如果已知曲线y=f(x),由(2)求出k,由(1)求出b,得到直线方程y=kx+b

  17. 2，水平渐近线y=b 当由(2)求出k=0时,这时 3, 竖直渐近线x=a 在这时,动点p距离原点将越来越远 渐近线是y=kx+b,则b=f(x)-kx的极限,k=f(x)/x的极限 渐近线是y=b,则k=0,所以b是x→∞时f(x)的极限. 渐近线是x=a,则k为无穷大,f(x)的极限为无穷大.

  18. 例4 求曲线的渐近线 解: 是曲线的斜渐近线 所以x=1是曲线的竖直渐近线

More Related