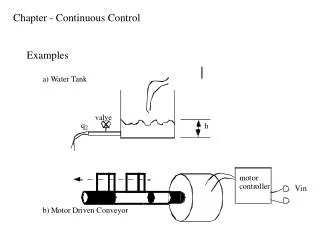
Structured H ∞ control of a continuous crystallizer
250 likes | 492 Vues
Structured H ∞ control of a continuous crystallizer. L. Ravanbod, D. Noll, P. Apkarian Institut de Mathématiques de Toulouse. IFAC Workshop on Control Distributed Parameter Systems Toulouse, France July 20-24, 2009. Outline. Industrial Crystallizer :

Structured H ∞ control of a continuous crystallizer
E N D
Presentation Transcript
Structured H∞control of a continuous crystallizer L. Ravanbod, D. Noll, P. Apkarian Institut de Mathématiques de Toulouse IFAC Workshop on Control Distributed Parameter Systems Toulouse, France July 20-24, 2009
Outline • Industrial Crystallizer : presentation, physical model. • WhyH∞ control? • H∞ control : structured controller, structured + time constraints. • Simulation results : application to continuous crystallizer.
Continuous Industrial Crystallizer used for mass production of high-purity solids from liquids. (e) a: body b: settling region of fine crystals c: slurry is withdrawn d: slurry heated and combined with product feed e: solvent evaporates (a) (b) (c) (d) This crystallizer produces hundreds of tons of amonium sulfate per day.
ideal mixing, • isothermal operation, • constant overall volume, • nucleation at negligible size, • size-independence growth rate, • no breakage, no agglomeration Continuous Crystallizer : Ourhypotheses • q: feed rate • Cf: solute concentration in feed • C: solute concentration • hf: classification function of fines dissolution • hp: classification function of product removal • n: number density function q, hf ,n, c q, cf q, hp, n, c
n L , t n L , t q G c h L h L n L , t f p t L v B c n L ,0 n L , n 0, t 0 G c g b G c K c t c , B c K c t c g s b s Continuous Crystallizer:equations =(number of crystals/crystal length L)/volume at time t Population balance: with initial and boundary conditions: growth rate nucleation (birth) rate and the classification functions:
q Mc dc q Mc Mc d f M dt v dt v q 3 1 K h L 1 n L , t L dL v v p 0 c 0 c 0 3 m L , t K n L , t L v 3 m t K n L , t L v 0 Continuous Crystallizer:equations mole balance : with initial condition: 3 t 1 K n L , t L dL and where: v 0 Crystal size distribution is represented by mass density function: and by overall crystal mass dL
Continuous Crystallizer:Why feedback control? • Nucleation, • crystal growth, • fines dissolution, • classified product removal • … Undesirable oscillatory behaviour As in solute concentration:
Continuous Crystallizer:Why feedback control? Or as in mass density function:
P: plant (crystallizer), K: controller w z P w(t) : u(t) : z(t) : y(t): u y Find structured controller i.e. K(s) ĸ(s): K ( Supω ) Control strategies • guarantying internal stability, • minimizing impact of on z w Two families of linear regulators: • if w white noise: • if w of finite energy:
H∞ control of crystallizer Previous works: Population balance finite or infinite dim.model finite dim. H∞ controller (SISO) (Chiu et al 1999, Bosgra et al 1995) (Vollmer and Raisch 2001) We propose: Population balance Large state linear model small dim. H∞ controller Advantage: • selection of controller structure, • easily extendable to MIMO, • time constraints conveniently added.
min K T K w z Constrained structured H∞ control Minimize: Subject to z t z K , t z t , for all t t t l u z K , s T K , s w s 0 w z K K Θ Time domain constraints, (w0(t) step, ramps, sinusoid) Θ decision variable
Multistage H∞ synthesis Closed-loop interconnection Non smooth optimization stabilizing 2nd order H∞controller stabilizing2nd order H∞ controller: time constraints satisfied Smooth optimization (SQP) Non smooth optimization stabilizing 2nd order H∞ controller: time constraints are approximately satisfied
H∞ controlNumerical method • H∞ synthesis is minmaxnonsmooth and nonconvex techniques is proposed: is handled through a progress function: minimized by Cutting-Plane Algorithm. Efficient for large systems due to possibility of structure selection ( Apkarian, Noll, Bompart, Rondepierre,…2006, 2007, 2008) • Smooth optimization (SQP) accelerates creation of good starting points. • Closed-loop stability is guaranteed by constraint:
1 2 3 solute concentration in the feed Cf(t) solute concentration in the liquid C(t) Cf(t) and disolution rate R1(t) C(t) and overall crystal mass M(t) 0mm 2mm Continuous Crystallizer:modelling Choosing the parameter values: KCl laboratory crystallizer used by : U. Vollmer, J. Raisch, Control Engineering Practice 2001 Model input, output choice • SISO • MIMO discretization of n(L,t) w.r.t L
4 5 Continuous Crystallizer:modelling Equidistant discretization with N=250, et mollifying the classification functions Linear model (for synthesis) Linearization at an equilibrium point with state space representation Equidistant discretization with N=1000 Nonlinear model (for validation)
SISO MIMO Simulation results(Input-Output Model precision)
Simulation resultsSISO : solute concentrations Second order H∞ controller+ time domain constraints
Simulation resultsMIMO: solute concentration, overall mass Second order H∞ controller+ constraints
Simulation resultsMass density • evolution in open-loop and in closed-loop • evolution from one equlibrium point to another one
Conclusion • New control methodology allows great flexibility of controller structure: small controllers for large systems. • Time constraints can be added and allow to include features of nonlinear systems. • Problem is genuinely nonsmooth and specific algorithm has to be developed.
Simulation resultsMIMO: solute concentration, overall mass PID H∞ controller+ time constraints
P: plant (crystallizer), K: controller w z P w(t) : u(t) : z(t) : y(t): u y K Objectif find K(s) ĸ(s): • internal stability, • minimizing impact of on z w Control strategies Two families of linear regulators can be found: • if w white noise: • if w of finite energy: