1 / 45

FORMULE TRIGONOMETRICHE

FORMULE TRIGONOMETRICHE. FORMULE TRIGONOMETRICHE.

nadine-burgess
Télécharger la présentation

FORMULE TRIGONOMETRICHE

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. FORMULE TRIGONOMETRICHE

  2. FORMULE TRIGONOMETRICHE Le funzioni goniometriche seno, coseno, tangente e cotangente sono usate normalmente ogni volta che è necessario descrivere come varia una grandezza fisica scalare in funzione della direzione e, più in generale, ogni volta che in un problema è coinvolto un angolo Ma hanno un «difetto», non sono proporzionali agli angoli; per esempio, il seno di 90° non è il triplo del seno di 30° altro esempio, la tangente di 90° non è il doppio della tangente di 45° . . . La tangente di 45° è 1 mentre quella di 90° è !!!!!

  3. FORMULE TRIGONOMETRICHE E’ fondamentale quindi avere a disposizione delle regole (formule) che possano permettere di calcolare il valore delle funzioni goniometriche partendo da particolari combinazioni di angoli Ad esempio: quanto vale il coseno di un angolo pari a a – b cos(a – b) se si conoscono cosa e cosb?

  4. FORMULE TRIGONOMETRICHE La risposta è cos(a – b) = sena senb + cosa cosb Come si ottiene questa relazione?

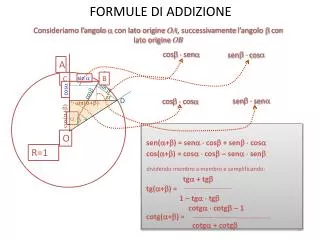
  5. FORMULE TRIGONOMETRICHE FORMULE DI ADDIZIONE E SOTTRAZIONE

  6. Coseno della differenza tra due angoli cos(a – b) y P’ a A 0 x

  7. P’ (cosa; sena) y P’ a A 0 x

  8. P’ (cosa; sena) y P P’ a b A 0 x

  9. P’ (cosa; sena) y P P (cosb; senb) P’ P a b A 0 x

  10. P’ (cosa; sena) y P P (cosb; senb) P’ P a - b a b A 0 x Quest’angolo in verde è a- b

  11. P’ (cosa; sena) y P P (cosb; senb) P’ P a - b A 0 x

  12. P’ (cosa; sena) y P P (cosb; senb) P’ P a - b A 0 x Scriviamo l’espressione della distanza P’P

  13. A B = (xb – xa)2 + (yb –ya)2 RIPASSO DISTANZA TRA DUE PUNTI IN UN SISTEMA DI ASSI CARTESIANI A (xa; ya) B(xb; yb) y B A 0 x

  14. P’ (cosa; sena) y P P (cosb; senb) P’ P a - b A 0 x Scriviamo l’espressione della distanza P’P

  15. P’ (cosa; sena) y P P (cosb; senb) P’ P a - b A 0 x Costruiamo lo stesso angolo (a – b) partendo dal punto A

  16. P’ (cosa; sena) y P P (cosb; senb) P’ P a - b x A 0 x Costruiamo lo stesso angolo a – b partendo dal punto A

  17. y K P P’ P a - b x A 0 x

  18. y K P P’ P a - b x 0 A A (1; 0) K [cos(a – b); sen(a – b)] La distanza AK è data da

  19. y K P P’ P a - b A x 0 PP’ = AK

  20. Coseno della somma tra due angoli cos(a + b)

  21. cos(a + b) = cos[a – (- b)] Applicando la relazione trovata in precedenza cos[a – (- b)] = senasen(- b) + cosacos(- b) e, poiché sen(- b) = - senb e cos(- b) = cosb y b x - b

  22. cos(a + b) = cos[a – (- b)] Applicando la relazione trovata in precedenza cos[a – (- b)] = senasen(- b) + cosacos(- b) e, poiché sen(- b) = - senb e cos(- b) = cosb y b x - b

  23. cos(a + b) = cos[a – (- b)] Applicando la relazione trovata in precedenza cos[a – (- b)] = senasen(- b) + cosacos(- b) e, poiché sen(- b) = - senb e cos(- b) = cosb y b x - b cos(a + b) = sena[- senb] + cosacosb = - senasenb + cosacosb • quindi

  24. Seno della somma tra due angoli sen(a + b)

  25. Seno della differenza tra due angoli sen(a - b)

  26. sen(a - b) = sen[a + (- b)] = = cosasen(- b) + sena cos(- b) = cosa[-senb] + sena cosb = sena cosb -cosasenb sen(a - b) = sena cosb-cosasenb

  27. FORMULE DI DUPLICAZIONE sen2a = ? cos2a = ? tg2a = ? cotg2a = ?

  28. FORMULE DI DUPLICAZIONE sen2a =sen(a + a) = cosasena + senacosa sen2a = 2senacosa

  29. FORMULE DI DUPLICAZIONE cos2a =cos(a + a) = cosacosa - senasena cos2a = cos2a - sen2a

  30. FORMULE DI DUPLICAZIONE Esercizio Utilizzando sen2a = 2senacosa cos2a = cos2a - sen2a Ricavare le formule di duplicazione per: tg2a e cotg2a

  31. FORMULE DI SOTTRAZIONE ESEMPIO DI APPLICAZIONE sen(a-b) = senacosb - senbcosa cos(a-b) = senasenb + cosbcosa

  32. FORMULE DI SOTTRAZIONE ESEMPIO DI APPLICAZIONE sen(a-b) = senacosb - senbcosa cos(a-b) = senasenb + cosbcosa

  33. FORMULE DI ADDIZIONE ESEMPIO DI APPLICAZIONE sen(a+b) = senacosb + senbcosa cos(a+b) = senasenb - cosbcosa

  34. FORMULE DI SOTTRAZIONE ESEMPIO DI APPLICAZIONE sen(a+b) = senacosb + senbcosa cos(a+b) = cosbcosa - senasenb

More Related