1 / 8

Trigonometry

This guide provides an overview of angles, degrees, and special triangles in trigonometry. It defines what constitutes an angle, addressing counterclockwise and clockwise rotations and their respective designations as positive or negative angles. The document covers key concepts like complementary and supplementary angles, and introduces the Pythagorean Theorem, highlighting the relationship between the legs and hypotenuse of right triangles. Special triangles, such as the 30-60-90 and 45-45-90 triangles, are discussed with their unique angle measures and side ratios.

nile
Télécharger la présentation

Trigonometry

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Trigonometry 1.1 Angles, Degrees, and Special Triangles

  2. An angle is formed by two rays with a common vertex. • Every angle has an initial and terminal side. • Counterclockwise rotation from initial to terminal side results in a positive angle • Such a rotation that is clockwise results in a negative angle. Angles in General

  3. Degree- • Complementary- • Supplementary- Degree Measure

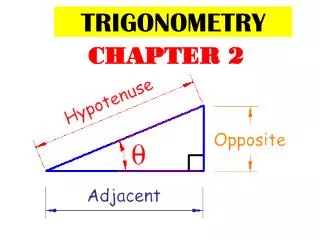
  4. For any right triangle, the sum of the squares of the legs equals the square of the hypotenuse. • Proof: See page 5 of text. Pythagorean Theorem

  5. Memorize this relationship. 30-60-90 Triangles 60° 2x x 90° 30° x

  6. 45-45-90 Triangles 45° x x 45° x

  7. Open the Socrative Student App, go to room #60306. Question 3 45° 10 m Quiz Questions 45° Question 4 60° 8 90° 30° y

  8. Page 10: 1-65 odds Assignment

More Related