Branch-and-bound

1. Branch-and-bound Jin Zheng, Central South University

2. Branch and Bound • An enhancement of backtracking • Similarity • A state space tree is used to solve a problem. • Difference • The branch-and-bound algorithm does not limit us to any particular way of traversing the tree and is used only for optimization problems • The backtracking algorithm requires the using of DFS traversal and is used for nonoptimization problems. Jin Zheng, Central South University

3. Branch and Bound • Compared to backtracking ,branch-and-bound requires two additional items. • A way to provide,for every node of a state-space-tree ,a bound on the best value of the objective function on any solution that can be obtained by adding further components to the partial solution represented by the node. • The value of the best solution seen so far. Jin Zheng, Central South University

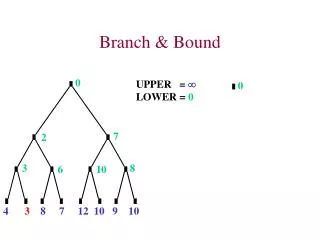
4. The main idea • Set up a bounding function, which is used to compute a bound (for the value of the objective function) at a node on a state-space tree and determine if it is promising • Promising (if the bound is better than the value of the best soluton so far:expand beyond the node. • Nonpromising (if the bound is no better than the value of the best solution so far--:not smaller for a minimization problem and not larger for a maxmization problem ): not expand beyond the node (pruning the state-space tree). Jin Zheng, Central South University

5. Terminate a search path at the current node in a state-space tree for any one of the following three reasons: • The value of the node’s bound is not better than the value of the best solution seen so far. • The node reprsents no feasible solutions because the constraints of the problem are already violated. • The subset of feasible solutions reprsented by the node consists of a single point(and hence no further choices can be made)-in this case we compare the value of the objective function for this feasible solution with that of the best solution seen so far and update the latter with the former if the new solution is better. Jin Zheng, Central South University

6. Assignment problem Job1 Job2 Job3 Job4 • 2 7 8 • 4 3 7 • 8 1 8 • 7 6 9 4 C= Jin Zheng, Central South University

7. 0 2 1 3 4 5 6 7 c￫3 Ib=13 Start Ib=10 a￫1 Ib=17 a￫2 Ib=10 a￫3 Ib=20 b￫3 Ib=14 b￫1 Ib=13 b￫4 Ib=17 c￫4 Ib=20 d￫4 Cost=13 a￫4 Ib=18 8 9 10 complete state-space tree for the instance of the assignment problem solved with the best-first branch-and-bound algorithm Jin Zheng, Central South University

8. Traveling Salesman Problem—Bounding Function 1 • Because a tour must leave every vertex exactly once, a lower bound on the length of a tour is the sum of the minimum (lower bound)cost of leaving every vertex. • The lower bound on the cost of leaving vertex v1 is given by the minimum of all the nonzero entries in row 1 of the adjacency matrix. • … • The lower bound on the cost of leaving vertex vn is given by the minimum of all the nonzero entries in row n of the adjacency matrix. • Note: This is not to say that there is a tour with this length. Rather, it says that there can be no shorter tour.Assume that the tour starts with v1. Jin Zheng, Central South University

9. Traveling Salesman Problem—Bounding Function 2 • Because every vertex must be entered and exited exactly once, a lower bound on the length of a tour is the sum of the minimum cost of entering and leaving every vertex. • For a given edge (u, v), think of half of its weight as the the exiting cost of u, and half of its weight as the entering cost of v. • The total length of a tour = the total cost of visiting( entering and exiting) every vertex exactly once. • The lower bound of the length of a tour = the lower bound of the total cost of visiting (entering and exiting ) every vertex exactly once. • Calculation: • for each vertex, pick top two shortest adjacent edges (their sum divided by 2 is the lower bound of the total cost of entering and exiting the vertex); • add up these summations for all the vertices. • Assume that the tour starts with vertex a and that b is visited before c. Jin Zheng, Central South University

10. a,b,c,d,e,a I=16 a,b,c Ib=16 a,b,c,d,e,a l=24 a,b,c,d,e,a l=19 a,b,c,d,e,a I=24 a,b,e Ib=19 a,b,d Ib=16 a,d Ib=16 a,c a,b Ib=14 a Ib=14 a,e Ib=19 Traveling salesman 0 3 2 4 1 5 6 7 b is not before c 8 10 9 11 Jin Zheng, Central South University

11. Notes • Finding a good bounding is not a simple task. • On the one hand.we want this function to be easy to compute. • On the other hand,it cann’t bt too simplistic.—otherwise,it would fail in its principal task to prune as many branches of a state-space tree as soon as possible. Jin Zheng, Central South University

12. 2 1 2 8 3 3 1 8 6 4 4 7 7 6 5 5 9 palace problem Jin Zheng, Central South University

13. 1 4 2 3 4 4 6 6 5 6 7 5 5 6 8 9 10 11 6 6 6 5 12 5 13 A solution 5 2 3 8 2 8 3 2 3 2 2 2 2 2 8 8 8 8 8 8 3 3 3 3 3 3 1 4 1 4 1 8 4 1 2 7 1 1 1 6 1 6 6 1 4 4 4 4 4 4 7 6 5 6 5 7 6 5 7 7 7 7 7 6 6 7 5 6 5 5 5 5 5 2 3 2 3 1 8 4 1 8 4 7 6 5 7 6 5 1 2 3 8 4 7 6 5 1 2 3 8 4 7 6 5 Jin Zheng, Central South University

14. Knapsack problem (1) v1/w1≥v2/w2 ≥… ≥vn/wn (2) bound function: ub=v+(W-w)(vi+1/wi+1) Jin Zheng, Central South University

15. Example Item weight value value/weight 1 4 40 10 2 7 42 6 3 5 25 5 4 3 12 4 • W=10 Jin Zheng, Central South University

16. w=0,v=0 Ub=100 w=4,v=40 Ub=76 w=0,v=0 Ub=60 w=11 w=4,v=40 Ub=70 w=9,v=65 Ub=69 w=4,v=40 Ub=64 w=12 w=9,v=65 Ub=65 W/o 1 With 1 Jin Zheng, Central South University