1 / 17

Polynomials and Polynomials Operations

Polynomials and Polynomials Operations. Grade 9 Math Bedford Junior High. A monomial is a constant or numerical coefficient , a variable or literal coefficient , or the product of a constant and one or more variables. A polynomial is the sum of one or more monomials.

robbin
Télécharger la présentation

Polynomials and Polynomials Operations

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Polynomials and Polynomials Operations Grade 9 Math Bedford Junior High

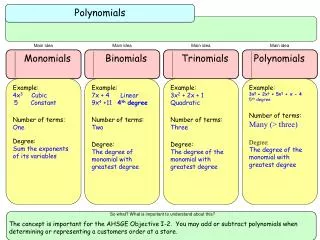
  2. A monomial is a constant or numerical coefficient, a variable or literal coefficient , or the product of a constant and one or more variables. A polynomial is the sum of one or more monomials. "... this means that a monomial is a single term which has NO positive sign (+) or negative sign (-) between entries.  It would be things like: 13, 3x, -57, x², 4y², -2xy, or  520x²y²  but NOT (2x+7) or (4x²-2x)." Polynomials: Monomials, Binomials, and Trinomials

  3. "A polynomial can be one monomial or a number of monomials grouped together with positive signs and/or negative signs.” The expression 3x² is a monomial because it has one term. The expression 5x² + 2x is a binomial because it has two terms. The expression  6x² +7x + 8 is a trinomial because it has three terms. All three expressions can be called polynomials.

  4. Adding Add like terms by adding the numerical coefficients.    ex.    4ab + -2ab = 2ab Subtracting Subtract one monomial from another like monomials, add the opposite of the second number. ex. 4ab - (-2ab) = 4ab +(+2ab)=6ab ex.    6x2 - x2 = 5x26x2 +(- x2) = 5x2 Operations with Polynomials

  5. Multiply monomials: Multiply the numerical coefficients. When variable factors are powers with the same base, multiply by adding exponent ex.    3x2(4x3) = 12x5 Because(3)(4) = 12 and ( x2)(x3)= x (2+3) = x5 Therefore 3x2(4x3) = 12x5 Divide monomials: Divide their numerical coefficients. When variable factors are powers with the same base, divide by subtracting exponents. ex.    30x21 (6x4) = 5x17 ( 30 ÷ 6) = 5 and x21 ÷ x4 = x17 Therefore, the answer is 5x17 Operations with Polynomials

  6. Distributive Property • Means that what is inside the bracket is affected by the outside term. • For example with a sharing model: 3 ( x + 2) this means we have 3 groups of ( x+ 2) Which would give us a total of 3x +6 v

  7. Distributive Property • Area Model • Remember that Area = length X width • 3( x +2) the (l) is 3 and (w) is (x+2) • Therefore 3( x +2) = 3x + 6

  8. Distributive Property Symbolically : The “3” affects each item inside the bracket. It does not matter how many terms are inside the bracket. Each term is affected 3 ( x+ 2) 3(x) + 3(2) 3x + 6 Another example is 7x( 2x + 4y): (7x) (2x) + (7x) (4y) (7)(2)(x)(x) + (7)(4)(x)(y) 14 x2 + 28xy

  9. Factoring Polynomial Expressions Symbolically ( Finding the GCF) Let’s say we have the following expression 35 a3 - 28 a2 + 21a we have to look for the greatest numerical coefficient and literal coefficient that can come out of each part of the expression. (7·5·a·a·a) - (4·7·a·a) + (3·7·a) Therefore, we find the factors of each term. “7” is common to all three terms as well as “a”. What is left over from the term goes inside the bracket. Our GCF is 7a . The leftovers are ( 5a2 - 4a + 3) . So our two factors are: ( 7a) ( 5a2 - 4a + 3)

  10. Factoring : We can use the distributive principle and the area model to check our answer. Our length is (7a) and our width is ( 5a2 - 4a + 3) . Therefore our area is 35 a3 - 28 a2 + 21a We are now back to where we started.

  11. When building a rectangular tile model, use the following guidelines: Begin at the top left corner with the x2 tiles ( Region 1) Construct a rectangle in the bottom right corner with the unit tiles ( Region 4) Fill the top right and bottom left with the x-tiles ( regions 2 and 3) If you draw a rectangle with a length of (x + 1) and width of ( x + 5) the area of the rectangle is : x2 +6x +5 Multiplying Two Binomials Region 1 x2 Region 2 X tiles Region 3 x tiles Region 4 Unit tiles

  12. Multiplying Two Binomials Using the Distributive Principle • Using the distributive principle you can do this symbolically as follows: • (x+3)(x+5) • (x)(x+5) +3(x+5) • (x)(x) + (x)(5) + (3)(x) + (3)(5) • x2 + 5x +3x + 15 ( Remember to combine like terms) • x2 + 8x + 15( final simplified version)

  13. (x+3)(x+5) Multiply the FIRST terms in each bracket Multiply the first term in the first set of brackets and the last term in the section set of brackets (OUTSIDE) multiply the last term in the first set of brackets and first term in the second set of brackets (INSIDE) multiply the last terms in each set of brackets. ( LAST) An acronym is FOIL ( x) ( x) = x2 (x) (5) = 5x (3)(x) = 3x ( 3) (5) = 15 Therefore we get x2 + 8x + 15 Another Way to Remember the Distributive Principle

  14. If you have one side of the rectangle positive and the other side negative, then using the distributive principle (x -2) ( x +3) X2 + 3x -2x -6 You need the pieces to complete all regions of your rectangle , but your final outcome will be : X2 + x - 6 because you use the ZERO Principle However, to have a complete rectangle , you NEED the pieces + 2x and -2x Multiplying Binomials with Negatives

  15. Factoring Trinomials • When you are factoring trinomials , you are organizing your tiles into a rectangle . Its side measures become your factors. • One way to help you find your side measures is to look at your unit tiles • If we were factoring X2 +7x +6 • We need to find two numbers whose sum is 7 and whose product is 6. • We list the pairs of factors of 6. We add each pair of factors . • Because we know thatx times x is x2, then our first part of the term in each bracket is ( x ) (x ) • We look for the factors that have the sum of 7 . They are 1 and 6. • We write these numbers as the second terms in the binomials. • X2 +7x +6 = ( x + 1 ) ( x + 6)

  16. More Factoring • If it was X2 +x -6 then it would have to be • ( x - 2 ) ( x + 3) because -2 time 3 equals -6 and -2 plus 3 equals +1 • One side of your rectangle must be positive and the other side must be negative. • Two positive and two negative create Zero , so we will have to put in two positive x’s and two negative x’s to complete the rectangle.

  17. If you are dividing a trinomial , then you can use the area model to help you find your answer. If you have x2 + 4x + 4 and you are dividing it by (x + 2) , you make one of your side measures (x + 2). Now you can start organizing your tiles into a rectangle . If one side is (x+2) then the other side MUST be (x+2) x2 + 4x + 4 = (x+2)(x+2) ( x + 2) = ( x + 2) Dividing Trinomials

More Related