1 / 5

Exploring Graphs of Quadratic and Cubic Functions: Equations and Key Features

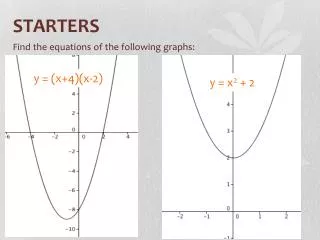
This guide covers finding equations for various quadratic and cubic graphs. Start with the quadratic equation y = (x + 4)(x - 2) and its equivalent y = x² + 2. Next, explore cubic functions, including y = x³ and its transformations. Learn about the point of inflection in cubic functions and how shifts affect their graphs. Example equations include y = x³ + 4, y = (x - 5)³ + 2, and y = (x + 1)³ - 2. Graphing these expressions reveals their unique characteristics and relationships.

roscoe
Télécharger la présentation

Exploring Graphs of Quadratic and Cubic Functions: Equations and Key Features

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. STARTERS Find the equations of the following graphs: y = (x+4)(x-2) y = x2 + 2

  2. Note 7: Cubics - Basic y = x3 This “central point” is called a “point of inflexion”

  3. Any functions of the basic cubic are treated the same as the shifts in the parabola. Examples: Graph y = x3 + 4 y = x3 + 4 y-intercept is 4

  4. Examples: Graph y = (x – 5)3 + 2 Vertex (5, 2) y = (x - 5)3 + 2

  5. Graph the following cubics y = x3 + 1 y = (x – 2)3 y = -x3y = (x + 1)3 – 2 y = x3– 3 y = (x – 3)3

More Related