Exploring Conditional Computational Entropy: Pseudo-Entropy and Pseudorandom Bit Extraction

1. ConditionalComputational Entropy Chun-Yuan Hsiao (Boston University, USA) Joint work with Chi-Jen Lu (Academia Sinica, Taiwan) Leonid Reyzin (Boston University, USA) Does Pseudo-Entropy = Incompressibility? How to extract more pseudorandom bits?

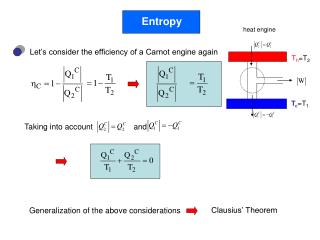
2. Shannon Entropy   H(X)Exx [log( Pr[X  x] )] X 2.58 bits Usually in crypto: minimum instead of average(a.k.a. min-entropy H(X) )

3.   means indistinguishable (in polynomial time) PRG (Blum-Micali-Yao) Pseudo-Entropy X has pseudo-entropykifY, H(Y) = kandX  Y HHILL(X) = k [Håstad,Impagliazzo,Levin,Luby] X Computational Entropy (version 1: HILL)

4. Entropy vs Compressibility Shannon's Theorem | X | = 60 H(X) = 40 H(X) X C(X) D(C(X)) = X  Compression length C(X) Compress (C) Decompress ( D)

5. Compression-Entropy Computational Entropy • X has computational entropy k, if we cannot efficiently compress X shorter than k HYao(X) = k [Yao82] • [Barak,Shaltiel,Wigderson03] gave min-entropy formulation (version 2: Yao) any subset of the support of X cannot be compressed

6. Computational Entropy • Version 1: HILL HHILL(X) = k, ifY, H(Y) = kandX  Y • Version 2: Yao HYao(X) = k, if we cannot efficiently compress X shorter than k   Question [Impagliazzo99]: Are these equivalent definitions?  ? ?

7. (Pseudo-)Entropy vs Compressibility Is computational analogue true? Recall Shannon’s Theorem:  ? pseudo- entropy compression length efficient

8. Computational Entropy • Version 1: HILL HHILL(X) = k, ifY, H(Y) = kandX  Y • Version 2: Yao HYao(X) = k, if we cannot efficiently compress X shorter than k   ?

9. Cryptographic Motivation pseudo H(X) randombits computational Extractor (Hashing) entropy  key Which computational entropy?all extractors work for HHILL(X);some work for HYao(X) [BSW03] e.g. gab If HYao(X) > HHILL(X) may get longer a key (by using the right extractor)

10. How? Our results 1.  distribution* X such that HYao(X) > HHILL(X) 2. bits extracted via HYao> bits extracted via HHILL 3. Define computational entropy, version 3: new, unpredictability-based definition 0. New† notion: conditional computational entropy†previously used, but never formalized *conditional distribution

11. Our Definition: ConditionalComputational Entropy • HILL: HHILL(X | Z)= k if  Y,H(Y | Z)= kand (X , Z)(Y , Z)  Z X Y ?

12. Our Definition: ConditionalComputational Entropy • Yao: HYao(X | Z)= k if we cannot efficiently compress X shorter than k Z Z D(C(X , Z) ,Z) =X C( X , Z)

13. Conditional is Everywhere in Crypto • In cryptography, adversaries usually have additional information • entropic secret: gab | adversary is givenga, gb • entropic secret: x | adversary is givenf(x) • entropic secret: SignSK(m)| adversary is givenPK • To make extraction precise, must talk about conditional entropy • Conditional computational entropy has been used implicitly in [Gennaro,Krawczyk,Rabin04],but never defined explicitly for HILL and Yao

14. Our results 0. New† notion: conditional computational entropy†previously used, but never formalized 1.  pair (X, Z) such that HYao(X | Z) >> HHILL(X | Z) (where Z is a uniform string) 2. Extract more pseudorandom bits from (X , Z) by considering its Yao-entropy 3. Define computational entropy, version 3: Hunp(X | Z) = k, if  efficient M, Pr[ M(Z) = X ] < 2k • Allows to talk about entropy of singletons, like x | f(x) • Can’t be defined unconditionally

15. Yao Entropy > HILL Entropy [Wee03] (oracle separation) [this paper] Length increasing random function f PRG G {0,1}n {0,1}3n X Caveat: need uniZK [Lepinski,Micali,Shelat05] X = ( G( Un ) ,  ) Z = NIZKreference string Non- Interactive Zero- Knowledge  Membership oracle m Yes No

16. Summary • Conditional Version 1: HHILL (X | Z) • Conditional Version 2: HYao (X | Z) • Conditional Version 3: Hunp (X | Z) Computational Entropy:    Can extract more from Yao than HILL(even unconditionally)

17. Thank You!