1 / 10

Solving One Step Inequalities by Adding

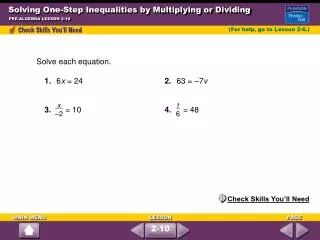
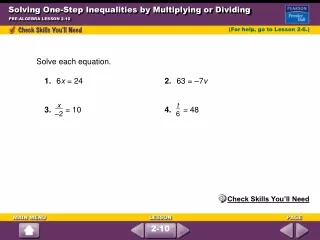
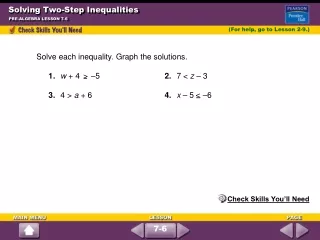
This guide provides a comprehensive overview of solving one-step inequalities through the concept of addition. It highlights the importance of converting subtraction into addition using its inverse and explains the Addition Property of Inequality: if a > b, then a + c > b + c, and if a < b, then a + c < b + c. Several examples are solved and graphed, including m + 3 > 6, 8 + t < 15, and -3 ≤ x + 7. A practical application, such as determining the weight limit for luggage, is also included, reinforcing these concepts with real-world context.

shadi
Télécharger la présentation

Solving One Step Inequalities by Adding

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Solving One Step Inequalities by Adding 2.9

  2. Reminder: KFC Turn all subtraction into addition of its inverse

  3. Addition Property of Inequality • If a>b, then a+c>b+c • If a<b, then a+c<b+c Works for –c or +c

  4. Solve and graph m+3>6

  5. Solve and graph: 8 + t <15

  6. Solve and graph: -3≤x+7

  7. Solve and graph: m-13>29

  8. Solve and graph: v – 4 ≤ 7

  9. An airline lets you check up to 65 lbs of luggage. One suitcase weights 37 lbs. How much can another suitcase weight? X+37≤65

  10. Homework • TB Pg 106 (8-28 even and #31)

More Related