1 / 18

Understanding Polynomials: Definitions, Like Terms, and the FOIL Method

This guide provides a comprehensive overview of polynomials, including definitions of key terms such as degree and like terms. A polynomial is described as an expression made of constants, variables, and exponents combined through addition, subtraction, and multiplication (not division). Learn how to identify like terms, add them by combining coefficients, and apply the FOIL method for multiplying polynomials. Practical examples illustrate how to execute these operations, helping you master polynomial concepts for homework and exams.

stacie
Télécharger la présentation

Understanding Polynomials: Definitions, Like Terms, and the FOIL Method

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

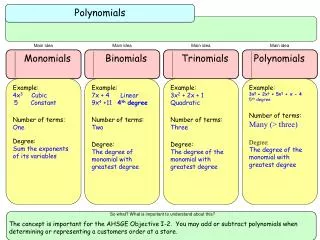
  1. 5.2 Polynomials Like terms FOIL method

  2. Definition of a Poly Poly- \Pol"y-\ [See Full, a.]A combining form or prefix from Gr. poly`s, many; as, polygon, a figure of many angles; polyatomic, having many atoms; polychord, polyconic. [1913 Webster] Also, polymorphic, polyester, polyamorous.

  3. Definition of a Polynomial A polynomial is an expression made with many constants, variables and exponents, which are combined using addition, subtraction and multiplication, ... but not division.

  4. Degree of a polynomial In a polynomial you find the terms with the highest exponent or addition of exponents; these would be the degree of the polynomial.

  5. Like Terms Terms that are fond of each other Terms with the same variable and exponent. 5x4y3 8x4y3 What can you do with like terms?

  6. Adding Like terms When you add like terms, you add their coefficients. 5x4y3 + 8x4y3 = (5 + 8)x4y3 = 13x4y3 You do not add the exponents. Why?

  7. Adding and Subtracting polynomials Add Remove the parentheses by distributing the number in front. In this case it is a one. Then add the like terms

  8. What about Subtracting

  9. Multiply Polynomials We use the distributive property to multiply a monomial times binomial, trinomial or any polynomial.

  10. Multiplying a binomial by a binomials Here we double distributive or more often call FOIL

  11. Multiply using FOIL (x – 5)(x + 2) x2 + 2x – 5x – 10 x2 -3x - 10

  12. Multiply using FOIL (x – 5)(x + 2) x2 + 2x – 5x – 10 x2 -3x - 10

  13. Multiply (x + 3)(x2 – 5x + 10)

  14. Multiply (x + 3)(x2 – 5x + 10) x3 – 5x2 + 10x

  15. Multiply (x + 3)(x2 – 5x + 10) x3 – 5x2 + 10x + 3x2 – 15x + 30

  16. Multiply (x + 3)(x2 – 5x + 10) x3 – 5x2 + 10x + 3x2 – 15x + 30 x3 -2x2 – 5x + 30

  17. Homework Page 231 – 232 # 17 – 33 odd, # 37 – 45 odd

  18. Homework Page 231 – 232 # 22 – 32 even, # 38 – 50 even

More Related