1 / 16

Quantum Fields for Cosmology in Precision Observations

Explore quantum fields in cosmology for improved precision, focusing on standard dynamics, new observables, interactions, and quantum effective actions. Understand the role of classical dynamics and the quantum effective potential in inflation and cosmological theories.

turner
Télécharger la présentation

Quantum Fields for Cosmology in Precision Observations

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Quantum fields for Cosmology Anders Tranberg Universityof Stavanger In collaborationwith Tommi Markkanen (Helsinki) JCAP 1211 (2012) 027/arXiv: 1207:2179 arXiv: 1303.0180 CPPP, Helsinki 4.-7. June 2013

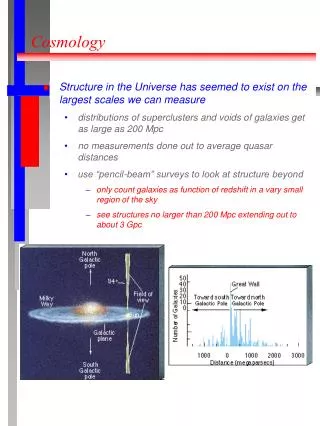
  2. Precision Cosmology • Unprecedentedprecision in observationsrequiresimprovedprecision in theoreticalpredictions and computations. Planck 2013! • Standard dynamics: • Inflation from classicallyslow-rolling homogeneousfield. • CMB from free, lightscalarfield modes in deSitterspacevacuum, freezing in semi-instantaneously at horizoncrossing. • New observables: • Non-gaussianity (bi-spectrum, tri-spectrum, spikes, …). • Scaledependencebeyondpowerlaw (spectralindex, running, runningofrunning…). • Efoldswithprecision +/- 10. • But: Inflaton is an interactingquantumfield.

  3. Corrections? Dynamics -> Value at horizoncrossing? Interactingvacuumstate? Dynamics -> End ofinflation -> valueof H(k)? Interactions -> high-order nontrivial correlators? Freeze-in afterhorizoncrossing? Reheatingdynamics -> H(k)? …

  4. Whatwe all know, butrarelystate. • The ”inflaton” is reallythemean-field (1-point function) of a quantumdegreeoffreedom (fundamental scalarfield, composite order parameter, …). • The ”potential” V is reallythequantumeffectivepotential, computed to some order in someexpansion. • Degreeoffreedomdisplaced from potential minimum -> inflation.

  5. Effectivepotential • 1) Lowenergyeffective action; integrateoutdegreesoffreedomabovesomeenergyscale -> effectiveinteractions for low-energydegreesoffreedom. • Ex. (Fermi theory <-> Electroweakinteractions, Standard Model <-> MSSM, …). • Still quantuminteractionsoflow-energydegreesoffreedom. • 2) Quantum effective action; integrateout all degreesoffreedomexceptthemeanfield/order parameter. • No more ”quantum” interactions. Treat as ”classical” dynamics in effectivepotential.

  6. Classical, classical and classical • Trulyclassicaltheory: no h-bar, noquantumfluctuations • Classicalequationsof motion • Toasters, macroscopicmagneticfields, gravity, cosmicstrings • Classicallimit.

  7. Classical, classical and classical • Classicalapproximation: • In a squeezedstate (largeoccupationnumbers), dynamicsareclassical-like. • Still need to average over ensemble representingthe initial state! • CMB-prescription: Replace ensemble average by average over the sky. Standby for Arttu’s talk! Starobinsky, Mukhanov, Garcia-Bellido, Grigoriev, Shaposhnikov, Tkachev, Smit, Serreau, Aarts, AT, Rajantie, Linde, Kofman, Hindmarsh, Felder, Saffin, Berges, Borsanyi, …

  8. Classical, classical and classical • Quantum effectivepotential: • Meanfieldevolutionfollows as ”classical” equationof motion from effectivepotential. • Meanfield~ ”theclassicalfield” (dangerous!) • Trulyclassical = trivial limit ofquantumeffectivepotential. • Computeeffective action: • Pickfavourite (renormalizable) tree-level action. • Compute diagrams untilyou run outofgraduate students. • Renormalize relative to somevacuum. • In real-time (in-in, CTP, Schwinger-Keldysh, …). Parker, Toms, Birrell, Davies, deWItt, Lyth, Shore, Shaposhnikov, Bezrukov, Barvinsky, Bilandzic, Prokopec, Kirsten, Elizalde, Enqvist, Lerner, Taanila, AT, Markkanen, Garbrecht, Postma…

  9. Quantum effective action in FRW • Example: One-loop 1PI effective action oftwocoupledscalarfieldsand metric. Treatmetric as classicalfield(nogravitational loops).

  10. Issues • Vacuum? • Identifyingdivergences -> anyvacuumcorrect to 4 derivatives (order H^4) is ok! • Useadiabaticvacuum? • Computing effective action? • Expansion in diagrams, and probably in gradients (adiabatic, Schwinger-deWitt, …). • Computeclose to whereyouneed it? • Renormalization? • Divergencesaregone. Applyrenormalizationconditions to fix parameters. • At whichscale? • To whichvalues? • Onlycounterterms for invariant operators.

  11. Quantum effective action in FRW • Most general case: Markkanen, AT: 2012

  12. Simplifiedmodel • Solve for . • Set: • Tree-level: 2 coupled, non-selfinteracting, minimallycoupledfields. Markkanen, AT: 2012

  13. Scalarfieldequationof motion • Given background (dS, mat. dom., rad. dom., …): Markkanen, AT: 2012

  14. Quantum correctedFriedmanneqs. • Self-consistentlysolving for thescalefactor: Markkanen, AT: 2012

  15. More issues • Infrared problems for masslessfields? • Becauseweuse ”perturbative” propagators, withmean-fieldinsertions. • Interactingtheory -> dynamicalmass. • End ofinflation? • Nonperturbativebehaviour (reheating, preheating, defects…). • Thermalization, imaginaryself-energies. • Needself-consistent, dynamicalpropagatorequation -> 2PI effective action. Calzetta, Hu, Cornwall, Jackiw, Tomboulis, … • Serreau 2011: 2PI-resummation to LO -> alwaysnon-zero mass in dS. (alsoBoyanovsky, deVega, Holman, Sloth, Riotto, Parentani, Garbrecht, Prokopec…) • LO is still Gaussian! NLO AT 2008 • Need a spacelatticeand a finitenumberof modes; all eventuallyredshiftintothe IR. Problem. AT 2008 • How to renormalizeconsistently?

  16. Conclusions • ModernCosmologicalobservationsareprecise to 10 (5?) e-folds. • Detectionof non-gaussianity is imminent (…maybe…). • For precisioncomputations, weneed to thinkoftheinflaton/curvaton as quantumfields. • Simple! Computetheeffectivepotential, and do as usual…maybewithout SR. • Useful! Onlyallowsrenormalizableinteractions-> restrictive (buteffectivetheories…). • Easy? Well…thetechniquesexist: • 1PI for massive fieldswithperturbativelysmallexcitations • 2PI for anyfieldswith non-perturbativelylargeexcitations. • -> alsoclassical-statisticalapproximation for verylargeexcitations.

More Related