Today’s agendum: Electric potential energy.

Today’s agendum: • Electric potential energy. • You must be able to use electric potential energy in work-energy calculations. • Electric potential. • You must be able to calculate the electric potential for a point charge, and use the electric potential in work-energy calculations. • Electric potential and electric potential energy of a system of charges. • You must be able to calculate both electric potential and electric potential energy for a system of charged particles (point charges today, charge distributions next lecture). • The electron volt. • You must be able to use the electron volt as an alternative unit of energy.

This lecture introduces electric potential energy and something called “electric potential.” Electric potential energy is “just like” gravitational potential energy. • Except that all matter exerts an attractive gravitational force, but charged particles exert either attractive or repulsive electrical forces—so we need to be careful with our signs. Electric potential is the electric potential energy per unit of charge. If you understand the symbols in the starting equations, and avoid sign and direction mistakes, homework and exams are not difficult.

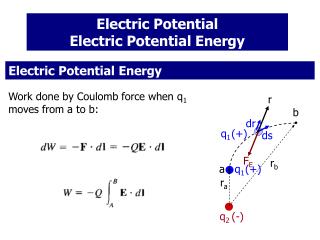
Electric Potential Electric Potential Energy Electric Potential Energy Work done by Coulomb force when q1 moves from a to b: r b dr q1(+) ds FE rb q1(+) a ra q2 (-) You don’t need to worry about the details of the math. They are provided for anybody who wants to study them later.

r b dr q1 (+) ds I did the calculation for a + charge moving away from a – charge; you could do a similar calculation for ++, -+, and ++. FE rb a ra q2 (-) The important point is that the work depends only on the initial and final positions of q1. In other words, the work done by the electric force is independent of path taken. The electric force is a conservative force. Disclaimer: this is a “demonstration” rather than a rigorous proof.

The next two slides are intended to draw a parallel between the electric and gravitational forces. Instead of saying “ugh, this is confusing new stuff,” you are supposed to say, “oh, this is easy, because I already learned the concepts in Physics 103.”

Consider an object of mass m in a gravitational field. It has potential energy U(y) = mgy and “feels” a gravitational force FG = GmM/r2, attractive. A bit of review: y If released, it gains kinetic energy and loses potential energy, but mechanical energy is conserved: Ef=Ei. The change in potential energy is Uf - Ui = -(Wc)if. Ui = mgyi yi Uf = 0 x What force does Wc? Force due to gravity. graphic “borrowed” from http://csep10.phys.utk.edu/astr161/lect/history/newtongrav.html

+ A charged particle in an electric field has electric potential energy. It “feels” a force (as given by Coulomb’s law). + + + + + + + + + + + + + + F E It gains kinetic energy and loses potential energy if released. The Coulomb force does positive work, and mechanical energy is conserved. - - - - - - - - - - - - - - - - - - -

The next two slides define electrical potential energy.

Now that we realize the electric force is conservative, we can define a potential energy associated with it. The subscript “E” is to remind you this is electric potential energy. After this slide, I will drop the subscript “E.” The change in potential energy when a charge q0 moves from point a to point b in the electric field of another charge q is r b dr q0 ds FE? rab a The minus sign in this equation comes from the definition of change in potential energy. The sign from the dot product is “automatically” correct if you include the signs of q and q0. ra ? on FE means the direction depends on the signs of the charges. q

(from the previous slide) is equivalent to your starting equation “i” and “f” refer to the two points for which we are calculating the potential energy difference. You could also use “a” and “b” like your text does, or “0” and “1” or anything else convenient. I use “i” and “f” because I always remember that (anything) = (anything)f – (anything)i. The next two slides use this definition of electrical potential energy to derive an equation for the electrical potential energy of two charged particles.

starting with an equation from two slides back… r b dr q0 ds FE? rab a ra By convention, we choose electric potential energy to be zero at infinite separation of the charges. this diagram shows q0 after it has moved from a to b q If there are any math majors in the room, please close your eyes for a few seconds. We should be talking about limits. 0 0

This provides us with the electric potential energy for a system of two point charges q and q0, separated by a distance r: You can call the charges q and q0, or q1 and q2, or whatever you want. If you have more than two charged particles, simply add the potential energies for each unique pair of particles. Example: calculate the electric potential energy for two protons separated by a typical proton-proton intranuclear distance of 2x10-15 m. What is the meaning of the + sign in the result?

Really Important fact to keep straight. The change in potential energy is the negative of the work done by the conservative force which is associated with the potential energy (the electric force). If an external force* moves an object “against” the conservative force, then Always ask yourself which work you are calculating. *for example, if you push two negatively charged balloons together

Electric Potential Previously, we defined the electric field by the force it exerts on a test charge q0: Similarly, it is useful to define the potential of a charge in terms of the potential energy of a test charge q0: The electric potential V is independent of the test charge q0.

From we see that the electric potential of a point charge q is The electric potential difference between points a and b is

Things to remember about electric potential:  Electric potential and electric potential energy are related, but are not the same. • Electric potential difference is the work per unit of charge that must be done to move a charge from one point to another without changing its kinetic energy.  The terms “electric potential” and “potential” are used interchangeably.  The units of potential are joules/coulomb:

Things to remember about electric potential:  Only differences in electric potential and electric potential energy are meaningful. • It is always necessary to define where U and V are zero. Here we defined V to be zero at an infinite distance from the sources of the electric field. • Sometimes it is convenient to define V to be zero at the earth (ground). • It should be clear from the context where V is defined to be zero, and I do not foresee you experiencing any confusion about where V is zero.

Two more starting equations: and so (potential is equal to potential energy per unit of charge) Potential energy and electric potential are defined relative to some reference point, so it is “better” to use

Two conceptual examples. Example: a proton is released in a region in space where there is an electric potential. Describe the subsequent motion of the proton. The proton will move towards the region of lower potential. As it moves, its potential energy will decrease, and its kinetic energy and speed will increase. Example: an electron is released in a region in space where there is an electric potential. Describe the subsequent motion of the electron. The electron will move towards the region of higher potential. As it moves, its potential energy will decrease, and its kinetic energy and speed will increase.

Electric Potential Energy of a System of Charges To find the electric potential energy for a system of two charges, we bring a second charge in from an infinite distance away: r q1 q1 q2 before after

To find the electric potential energy for a system of three charges, we bring a third charge in from an infinite distance away: r12 r12 q1 q2 q1 q2 r13 r23 q3 before after

Electric Potential and Potential Energy of a Charge Distribution Collection of charges: P is the point at which V is to be calculated, and ri is the distance of the ith charge from P. Charge distribution: dq r P Potential at point P.

Example: a 1 C point charge is located at the origin and a -4 C point charge 4 meters along the +x axis. Calculate the electric potential at a point P, 3 meters along the +y axis. y P 3 m x q2 q1 4 m

Example: how much work is required to bring a +3C point charge from infinity to point P? An external force moves q3slowly from an infinite distance to the point P. 0 y q3 P 0 3 m x q2 4 m q1 The work done by the external force was negative, so the work done by the electric field was positive. The electric field “pulled” q3 in (keep in mind q2 is 4 times as big as q1). Positive work would have to be done by an external force to remove q3 from P.

Example: find the total potential energy of the system of three charges. y q3 P 3 m x q2 4 m q1

The Electron Volt An electron volt (eV) is the energy acquired by a particle of charge e when it moves through a potential difference of 1 volt. This is a very small amount of energy on a macroscopic scale, but electrons in atoms typically have a few eV (10’s to 1000’s) of energy.

Today’s agendum: • Electric potential of a charge distribution. • You must be able to calculate the electric potential for a charge distribution. • Equipotentials. • You must be able to sketch and interpret equipotential plots. • Potential gradient. • You must be able to calculate the electric field if you are given the electric potential. • Potentials and fields near conductors. • You must be able to use what you have learned about electric fields, Gauss’ “Law”, and electric potential to understand and apply several useful facts about conductors in electrostatic equilibrium.

Electric Potential of a Charge Distribution Example: potential and electric field between two parallel conducting plates. Assume V0<V1 (so we can determine the direction of the electric field). Also assume the plates are large compared to their separation, so the electric field is constant and perpendicular to the plates. Also, let the plates be separated by a distance d. E V0 V1 d

y x E z dl V0 V1 d I’ll discuss in lecture why the absolute value signs are needed.

did not require rectangular plates, or any plates at all. It works as long as E is uniform. In general, E should be replaced by the component of along the displacement vector . Important note: the derivation of

Example: A rod of length L located along the x-axis has a total charge Q uniformly distributed along the rod. Find the electric potential at a point P along the y-axis a distance d from the origin. y =Q/L P r dq=dx d dq x dx x L

y A good set of math tables will have the integral: P r d dq x dx x L

Example: Find the electric potential due to a uniformly charged ring of radius R and total charge Q at a point P on the axis of the ring. dq Every dq of charge on the ring is the same distance from the point P. r R P x x

Could you use this expression for V to calculate E? Would you get the same result as we obtained previously? dq r R P x x

dq r a P  x  dE

Example: A disc of radius R has a uniform charge per unit area  and total charge Q. Calculate V at a point P along the central axis of the disc at a distance x from its center. dq The disc is made of concentric rings. The area of a ring at a radius r is 2rdr, and the charge on each ring is (2rdr). r P x x R We can use the equation for the potential due to a ring, replace R by r, and integrate from r=0 to r=R.

dq r P x x R

Could you use this expression for V to calculate E? dq r P x x R

See your text for other examples of potentials calculated from charge distributions, as well as an alternate discussion of the electric field between charged parallel plates.

PRACTICAL APPLICATION For some reason you think practical applications are important. Well, I found one!

Equipotentials Equipotentials are contour maps of the electric potential. http://www.omnimap.com/catalog/digital/topo.htm

Equipotential lines are another visualization tool. They illustrate where the potential is constant. Equipotential lines are actually projections on a 2-dimensional page of a 3-dimensional equipotential surface. (“Just like” the contour map.) The electric field must be perpendicular to equipotential lines. Why? Otherwise work would be required to move a charge along an equipotential surface, and it would not be equipotential. In the static case (charges not moving) the surface of a conductor is an equipotential surface. Why? Otherwise charge would flow and it wouldn’t be a static case.

Here are some electric field and equipotential lines I generated using an electromagnetic field program. Equipotential lines are shown in red.

Today’s agendum: Electric potential energy.