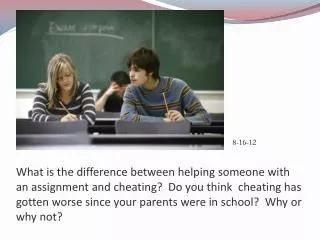
Преобразуване на цели числа в 2, 8, 16-ична бройна система

1. Преобразуване на цели числа в 2, 8, 16-ична бройна система десетична шестнадесетична 0123456789 0123456789ABCDEF 01234567 01 двoична осмична

2. Да вземем произволно десетично число, например 46, и за него да изпълним всички възможни последователни преобразувания от една бройна система в друга 46 10 56 2E 8 16 2 101110 2E 46 10 101110 56 101110 2 16 8 2 8 16 10 10 56 2E 46 46

3. Представяне на числата в различните бройни системи: • В десетична: 756=1.102+5.101+6.100 • В двоична бр. система числата се представят по подобен начин: 1101(2) = 1.23+1.22+0.21+1.20 = 8 + 4 + 0 + 1 = 13(10) “десетичното число 13 е равно на двоичното число 1101”

4. Превръщане на числа от десетична в двоична бр. с-ма. • 74(10) = Х(2) • 74:2 = 37, остатък 0 • 37:2 = 18, остатък 1 • 18:2 = 9, остатък 0 • 9:2 = 4, остатък 1 • 4:2 = 2, остатък 0 • 2:2 = 1, остатък 0 • 1:2 = 0, остатък 1 Числото се дели на две до получаване на 0!!! Остатъците при деление се записват в обратен ред и това е числото в дв. бр. с-ма. Проверка: 1001010(2) = 26+23+21= 64 + 8 + 2 = 74(10) 74(10) = 1001010(2)

5. Преобразуване на числата (8)  (2), (16)  (2) • Преобразуване на осмични и шестнадесетични числа в двоична система: всяка цифра заменяме с еквивалентната и двоична триада (тройка цифри) или тетрада (четворка цифри). • Примери : 53718 = 101 011 111 0012; 5 3 7 1 1A3F16 = 1 1010 0011 11112 1 A 3F

6. Преобразуване на числата (2)  (8), (2)  (16) • За да преобразуваме число от двоична система в осмична или шестнадесетична, е необходимо да го разделим вляво и вдясно от запетаята на триада (за осмичната) или тетрада (за шестнадесетичната) и всяка такава група да заменим със съответната осмична (шестнадесетична) цифра. Примери: 11010100001112 = 1 5 2 0 78; 1101010000111 1101110000011012 = 6 E 0 D16 110 1110 0000 1101 • Преобразувайте : 10111110101011002 = 10110101000001102 =

7. За по-добро усвояване на двоичната бройна система е необходимо да се усвои изпълнението на аритметическите действия с двоични числа. Всички позиционни бройни системи са ”еднакви”, а именно, при всички тях аритметическите операции се извършват по едни и същи правила: • В сила са същите закони на аритметиката: Комутативен закон : a + b = b + a, a b = b a Асоциативен закон : a + (b + c) = (a + b) + c, a (b c) = (a b) c Дистрибутивен закон : a(b + c) = ab + ac • В сила са правилата за събиране, изваждане, умножение и деление по колони; • Правилата за извършване на аритметическите операции се опират на таблиците за събиране и умножение.

8. Събиране Правила за събиране: 0+0=0 1+0=1 0+1=1 1+1=10 (резултатът от събирането на две единици: нула и единица пренос в старшия разряд)

9. Събирането на двоични числа се извършва в колони Примери: 10110 1001 1111 101,011 + 101 + 1010 + 1 + 1,11 11011 10011 10000 111 ,001

10. Умножение Правила за умножение: 0*0=0 1*0=0 0*1=0 1*1=1

11. Умножението на двоични числа се извършва в колони аналогично на умножението на десетичните числа. Примери: 1011 1101 *101 *11 + 1011 1101 1011 +1101 110111 100111

12. Изваждане Правила за изваждане: 0-0=0 1-0=1 1-1=0 10-1=1(от нула не може да се изважда единица, затова при изваждане е необходимо да се вземе единица от старшия разряд)

13. При изпълнение на операцията изваждане винаги от по-голямото по абсолютна стойност се изважда по-малкото и на резултата се поставя съответния знак. Примери: 1011 1001 11-1011= -(1011-11) -111 -110 1011 100 11 - 11 1000

14. Деление Делението в двоична бройна система се извършва, както и в десeтична бройна система. Пример: 10101 111 - 111 11 111 - 111 0

15. Затвърждаване на изученото №1 Извършете събирането: №2 Извършете умножението: • 100101+101= 1) 100001*10010= • 101101+111= 2) 110001*1011= • 11001,1+11,01= 3) 101*101= №3 Извършете изваждането: №4 Извършете делението: • 1000101-1010= 1) 10000:10= • 1101101-110= 2) 101101:101= • 110101-101= 3) 100011:11= Отговори

16. Отговори №1 Извършете събирането : №2 Извършете умножението : • 100101+101= 101010 1) 100001*10010=1001010010 • 101101+111= 110100 2) 110001*1011=1000011011 • 11001,1+11,01=11100,11 3) 101*101=11001 №3 Извършете изваждането : №4 Извършете делението : • 1000101-1010= 111011 1) 10000:10=100 • 1101101-110= 1100111 2) 101101:101=1001 • 110101-101= 110000 3) 100011:11=1011

17. Домашна работа: 1. Изучете правилата за извършване на аритметическите действия в двоична бройна система. 2. Извършете действията: • 110010+1101 • 1111001-1101 • 101011*11 • 10101110:101