× × × × × × × × × × × × × × × ×
120 likes | 258 Vues
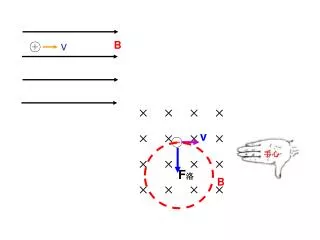
× × × × × × × × × × × × × × × ×. v. B. +. 手心. v. -. B. F 洛. θ 2 π. t=T. O. θ. v. 复习与巩固. 当v ∥ B时,带电粒子不受磁场力, F 洛 =0 ; 当v ⊥ B时,带电粒子受洛伦兹力 F 洛 =qvB ; 当V与B有夹角 θ时,分解B用 F 洛 =qvB ⊥. qvB=mv 2 /r. r=mv/qB. T=2 πr/v= 2 π m/qB.

× × × × × × × × × × × × × × × ×
E N D
Presentation Transcript
× × × × × × × × × × × × × × × × v B + 手心 v - B F洛
θ 2π t=T O θ v 复习与巩固 • 当v∥B时,带电粒子不受磁场力,F洛=0; • 当v⊥B时,带电粒子受洛伦兹力F洛=qvB; • 当V与B有夹角θ时,分解B用F洛=qvB⊥ qvB=mv2/r r=mv/qB T=2πr/v=2πm/qB 若θ=60˚=π/3 则 t=T/6
带电粒子小结 e 3m 2e 23m e
1 2 1 B mv2-0=qU 练习1 • 已知氘核(d)、氚核(t)、氦原子核(α粒子)经过同一电场加速后同时进入同一匀强磁场中做匀速圆周运动,试判断它们三个的运动半径之比rd∶rt∶rα=∶ ∶ . qvB=mv2/r mv qB r= =
带电粒子在匀强磁场中的运动 原理:——洛伦兹力提供向心力—— 任务:求半径,求周期,求时间 关键:画粒子运动轨迹——求运动时间
速度方向向外 v (3)判断磁场方向 · · · · · · · · · · · · v B B F F F洛 B 练习2 (2)判断粒子的受力方向 (1)判断粒子运动方向 (4)判断电性
F B r V + m , q 练习3 • 在磁场中画出粒子的轨迹 O·
LBq m(1-cosθ) L (1-cosθ) 2πm Bq 左手不符,负电 θ 2π r = F F 练习4 已知粒子m、q,从M点进入匀强磁场B,从b点射出,磁场高L,射出时有θ, 1、判断粒子的电性; 2、求粒子在磁场中运动的时间; 3、求粒子的运动速度。 M N m,q 看几何关系,有: (r-L)/r=cosθ × × × × B L × × × × b Q P θ O· 又qvB=mv2/r v=
m,q v r M N F B × × × a × × × P ·Q b 练习5 • 带电粒子从M点射入有界(MNPQ)匀强磁场,从Q点射出,a、b已知 • (1)确定圆心位置,画运动轨迹 • (2)求运动半径r 看几何关系, 未知角度,用 (r-a)2+b2=r2 a2+b2 2a r= O· 若已知m、q、B,可以求v 记清用垂直平分线呀!
θ θ M M P P B B v a × × × × × × × × v a × × × × × × × × N N d d Q Q 练习6 带电粒子(负电)从a点垂直于MN进入匀强磁场(宽d),已知运动轨迹与PQ相切,试确定圆心,画运动轨迹。 O· ·O r+rcosθ=d
P S N a M b 60º v1 作业1 1、如图所示, 有界匀强磁场边界线SP∥MN, 速率不同的同种带电粒子从S点沿SP方向同时射入磁场. 其中穿过a点的粒子, 速度v1与MN垂直, 穿过b点的粒子, 速度v2与MN成60°角, 设二粒子从S到a, b所需时间分别为t1, t2. 则t1:t2为(重力不计) A. 1:3 B. 4:3 C. 1:1 D. 3:2
M B O v N 作业2 • 2.如下图所示, 分界面MN右侧是区域足够大的匀强磁场区, 现由O点射入两个速度、电量、质量都相同的正、负电粒子, 重力不计, 射入方向与分界面成θ角,则( ) A. 它们在磁场中运动时间相同 B. 它们在磁场中做圆运动的半径相同 C. 它们到达分界面的位置与O点距离相同 D. 它们到达分界面时速度方向相同