1 / 21

INSCRIBED ANGLES

INSCRIBED ANGLES. PROBLEM 1a. PROBLEM 1a. CONGRUENT AND INSCRIBED. INSCRIBED TO A SEMICIRCLE. PROBLEM 2. INSCRIBED AND CIRCUMSCRIBED. PROBLEM 3. PROBLEM 4. END SHOW. Standard 21:

zenaida-buck
Télécharger la présentation

INSCRIBED ANGLES

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. INSCRIBED ANGLES PROBLEM 1a PROBLEM 1a CONGRUENT AND INSCRIBED INSCRIBED TO A SEMICIRCLE PROBLEM 2 INSCRIBED AND CIRCUMSCRIBED PROBLEM 3 PROBLEM 4 END SHOW

  2. Standard 21: Students prove and solve problems regarding relationships among chords, secants, tangents, inscribed angles, and inscribed and circumscribed polygons of circles. Los estudiantes prueban y resuelven problemas relacionados con cuerdas, secantes, tangentes, ángulos inscritos y polígonos inscritos y circunscritos a círculos.

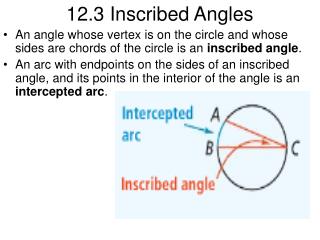
  3. Inscribed angles are angles formed by two chords whose vertex is on the circle. A Ángulos inscritos son ángulos formados por dos cuerdas cuyo vértice esta en el circulo B C ABC KML If an angle is inscribed in a circle then the measure of the angle equals one-half the measure of its intercepted arc. K m KL 1 2 Si un ángulo en un círculo es inscrito entonces la medida de el ángulo es igual a la mitad de su arco intersecado. M L m is an inscribed angle =

  4. = (40°) BAC 3 3 m BC 1 1 2 2 m A (3x+5)° B 40° (3X+5) = C 3X + 5 = 20 -5 -5 3X = 15 X=5

  5. K J (2x+7)° = 54° (54°) L JKL 2 2 m JL 1 1 2 2 m (2X+7) = 2X + 7 = 27 -7 -7 2X = 20 X=10

  6. A AB B P D C ADB ACB ADB ACB and intercept same arc If then If two inscribed angles of a circle or congruent circles intercept congruent arcs, or the same arc, then the angles are congruent. Si dos ángulos inscritos de un círculo o de círculos congruentes intersecan el mismo arco o arcos congruentes entonces los ángulos son congruentes.

  7. AC P A 90° m C B ABC ABC= intercepts semicircle If then If an inscribed angle intercepts a semicircle, then the angle is a right angle. Si un ángulo inscrito interseca a un semicírculo entonces el ángulo es recto.

  8. N = 90° 4X° K L M (6X-10)° 10 10 + (6X-10)° 4X° 10X-10 = 90 +10 +10 10X = 100 X=10

  9. These are concentric circles and all circles are similar. Estos son círculos concéntricos y todos los círculos son semejantes.

  10. K N L M A B P D C E F Q G H

  11. A B P D C E F X Q K G H R N g L M Quadrilateral ABCD is inscribed to circle P. Cuadrilatero ABCD esta inscrito al círculo P. Line g is TANGENT to circle X at point R. Línea g es tangente al círculo X en punto R. Quadrilateral EFGH is circumscribed tocircle Q, having sides to be TANGENT at points K, L, M and N. Cuadrilátero EFGH esta circunscrito al círculo Q, teniendo los lados TANGENTES en los puntos K, L, M y N.

  12. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F 4X+10 and = m -3X+45 = m Find the following: = ? m 1. ED B E I H G C D EBF EBD

  13. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F 4X+10 and = m -3X+45 = m Find the following: = ? m 1. ED B E I H G C D EBF EBD

  14. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F 4X+10 and = m -3X+45 = m Find the following: = ? m 1. ED B E I H G C D EBF EBD

  15. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F = 4X+10 and = m -3X+45 = m Find the following: 60° = ? m 30° 1. ED B E I H 30° G 60° 90° EFB EDB C and FGDE is a rhombus so all sides D are congruent because the F Reflexive Property EFB EBD EFB EBF EBD EBF EBF EBF EBD EBD EBF EDB EFB E B E B = 30° =-3X+45 m m m m m m =-3( )+45 EAB D EB EB EF ED -7 -7 Since is inscribed to SEMICIRCLE then are right, and then and ; and therefore then: by HL. And by CPCTC. 30° 60° So: Then = -3X+45 = 4X+10 60° 30° -45 -45 5 -3X = 4X – 35 = -15+45 -4X -4X =30° - 7X = - 35 So: Take notes X=5

  16. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F 4X+10 and = m -3X+45 = m 60° Find the following: B E I H G C D (2) (2) 30° = EBD EBD EBF = m ? 2. FE m m m m m ED ED FE ED ED 1 1 1 2 2 2 FE ED m EFED = ? m 30° 1. ED 60° If = 60° 30° 60° then: 30° = = 60° = 60° Since then and

  17. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F = = = 4X+10 and = m -3X+45 = m Find the following: B E I 60° H G C D (2) (2) 30° = EBD EBF BGD BED EBD BED = m ? 2. FE m m m m m FE ED ED ED ED 1 1 1 4. 3. ? ? 60° 2 2 2 FE ED m m m m EFED 60° = ? m 30° 1. ED 60° If = 60° 30° 60° then: 30° = = 60° = 60° Since then and From figure

  18. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F = = = = = = 4X+10 and = m -3X+45 = m Find the following: B E I 60° H G C D (2) (2) 30° = DEG BGD EGD BGD BGD BED EBD BED EBF EBD BGD = m ? 2. FE m m m m m ED ED ED FE ED 1 1 1 3. 4. ? ? 60° 2 2 2 FE ED m m m m m m = m DGE because EFGD is a rhombus m 180° + m m EFED 180° 60° + 120° 60° = ? m 30° 1. ED 60° If = 60° 30° 60° then: 30° = = 60° = 60° Since then and From figure and then Take notes -60° -60°

  19. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F 4X+10 and = m -3X+45 = m Find the following: B E I H G m 5. DB = 120° C D EBD EBF 60° 120° 60° 120°

  20. Inscribed to circle G are quadrilaterals EFBD and EABC, and quadrilaterals EFGD and GABC are rhombi. A F 120° 4X+10 and = m -3X+45 = m Find the following: B E I H G m 5. DB = C D 90° 7. = AIB EBD EBF m = 6. m DEB 60° 120° 60° 60°+60°+120° 120° = 240°

  21. Reasons Statements = a. a. Alternate interior are b. b. have the same measure c. c. S d. d. = e. e. = f. f. An inscribed is half its intercepted arc ABD CDB CDB ABD ABD CDB DC DC AB AB = g. h. g. h. = m m BC AD m m m m AD BC AD BC 1 1 1 1 Arcs with the same measure are 2 2 2 2 AD BC AD BC m m An inscribed is half its intercepted arc S m m B C Given A D Given: Prove: Transitive Property. Division Property of Equality

More Related