1 / 43

Geometry Chapter 6

Geometry Chapter 6. Quadrilaterals Kites and Trapezoids. Warm Up Solve for x. 1. x 2 + 38 = 3 x 2 – 12 2. 137 + x = 180 3. 4. Find FE. 5 or –5. 43. 156. Your Math Goal Today is…. Use properties of kites to solve problems. Use properties of trapezoids to solve problems.

adlai
Télécharger la présentation

Geometry Chapter 6

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Geometry Chapter 6 Quadrilaterals Kites and Trapezoids

  2. Warm Up Solve for x. 1.x2 + 38 = 3x2 – 12 2. 137 + x = 180 3. 4. Find FE. 5 or –5 43 156

  3. Your Math Goal Today is… Use properties of kites to solve problems. Use properties of trapezoids to solve problems.

  4. Vocabulary kite trapezoid base of a trapezoid leg of a trapezoid base angle of a trapezoid isosceles trapezoid midsegment of a trapezoid

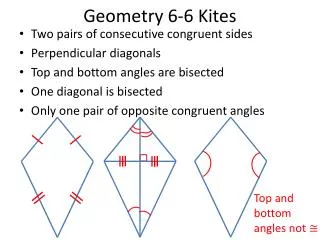
  5. A kiteis a quadrilateral with exactly two pairs of congruent consecutive sides.

  6. Example 1: Problem-Solving Application Lucy is framing a kite with wooden dowels. She uses two dowels that measure 18 cm, one dowel that measures 30 cm, and two dowels that measure 27 cm. To complete the kite, she needs a dowel to place along . She has a dowel that is 36 cm long. About how much wood will she have left after cutting the last dowel?

  7. 1 Make a Plan Understand the Problem The diagonals of a kite are perpendicular, so the four triangles are right triangles. Let N represent the intersection of the diagonals. Use the Pythagorean Theorem and the properties of kites to find , and . Add these lengths to find the length of . 2 Example 1 Continued The answer will be the amount of wood Lucy has left after cutting the dowel.

  8. 3 Solve Example 1 Continued N bisects JM. Pythagorean Thm. Pythagorean Thm.

  9. Example 1 Continued Lucy needs to cut the dowel to be 32.4 cm long. The amount of wood that will remain after the cut is, 36 – 32.4  3.6 cm Lucy will have 3.6 cm of wood left over after the cut.

  10. To estimate the length of the diagonal, change the side length into decimals and round. , and . The length of the diagonal is approximately 10 + 22 = 32. So the wood remaining is approximately 36 – 32 = 4. So 3.6 is a reasonable answer. 4 Example 1 Continued Look Back

  11. In Your Notes What if...?Daryl is going to make a kite by doubling all the measures in the kite. What is the total amount of binding needed to cover the edges of his kite? How many packages of binding must Daryl buy?

  12. 1 Understand the Problem In Your Notes • The answer has two parts. • • the total length of binding Daryl needs • • the number of packages of binding Daryl must buy

  13. Make a Plan 2 In Your Notes The diagonals of a kite are perpendicular, so the four triangles are right triangles. Use the Pythagorean Theorem and the properties of kites to find the unknown side lengths. Add these lengths to find the perimeter of the kite.

  14. 3 Solve perimeter of PQRS = In Your Notes Pyth. Thm. Pyth. Thm.

  15. packages of binding In Your Notes Daryl needs approximately 191.3 inches of binding. One package of binding contains 2 yards, or 72 inches. In order to have enough, Daryl must buy 3 packages of binding.

  16. To estimate the perimeter, change the side lengths into decimals and round. , and . The perimeter of the kite is approximately 2(54) + 2 (41) = 190. So 191.3 is a reasonable answer. 4 In Your Notes Look Back

  17. Example 2A: Using Properties of Kites In kite ABCD, mDAB = 54°, and mCDF = 52°. Find mBCD. Kite cons. sides  ∆BCD is isos. 2  sides isos. ∆ isos. ∆base s  CBF  CDF mCBF = mCDF Def. of  s Polygon  Sum Thm. mBCD + mCBF + mCDF = 180°

  18. Example 2A Continued mBCD + mCBF + mCDF = 180° Substitute mCDF for mCBF. mBCD + mCBF+ mCDF= 180° Substitute 52 for mCBF. mBCD + 52°+ 52° = 180° Subtract 104 from both sides. mBCD = 76°

  19. Example 2B: Using Properties of Kites In kite ABCD, mDAB = 54°, and mCDF = 52°. Find mABC. ADC  ABC Kite  one pair opp. s  Def. of s mADC = mABC Polygon  Sum Thm. mABC + mBCD + mADC + mDAB = 360° Substitute mABC for mADC. mABC + mBCD + mABC+ mDAB = 360°

  20. Example 2B Continued mABC + mBCD + mABC + mDAB = 360° mABC + 76°+ mABC + 54° = 360° Substitute. 2mABC = 230° Simplify. mABC = 115° Solve.

  21. Example 2C: Using Properties of Kites In kite ABCD, mDAB = 54°, and mCDF = 52°. Find mFDA. CDA  ABC Kite  one pair opp. s  mCDA = mABC Def. of s mCDF + mFDA = mABC Add. Post. 52° + mFDA = 115° Substitute. mFDA = 63° Solve.

  22. In Your Notes In kite PQRS, mPQR = 78°, and mTRS = 59°. Find mQRT. Kite cons. sides  ∆PQR is isos. 2 sides  isos. ∆ RPQ  PRQ isos. ∆base s  mQPT = mQRT Def. of s

  23. In Your Notes mPQR + mQRP + mQPR = 180° Polygon  Sum Thm. Substitute 78 for mPQR. 78° + mQRT+ mQPT = 180° 78° + mQRT + mQRT = 180° Substitute. 78° + 2mQRT = 180° Substitute. Subtract 78 from both sides. 2mQRT = 102° mQRT = 51° Divide by 2.

  24. In Your Notes In kite PQRS, mPQR = 78°, and mTRS = 59°. Find mQPS. QPS  QRS Kite  one pair opp. s   Add. Post. mQPS = mQRT + mTRS mQPS = mQRT + 59° Substitute. mQPS = 51° + 59° Substitute. mQPS = 110°

  25. In Your Notes In kite PQRS, mPQR = 78°, and mTRS = 59°. Find each mPSR. Polygon  Sum Thm. mSPT + mTRS + mRSP = 180° mSPT = mTRS Def. of s mTRS + mTRS + mRSP = 180° Substitute. 59° + 59°+ mRSP = 180° Substitute. Simplify. mRSP = 62°

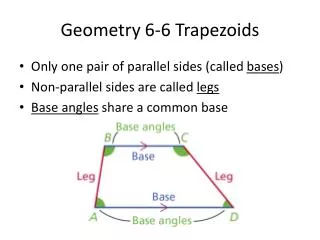
  26. A trapezoidis a quadrilateral with exactly one pair of parallel sides. Each of the parallel sides is called a base. The nonparallel sides are called legs. Baseanglesof a trapezoid are two consecutive angles whose common side is a base.

  27. If the legs of a trapezoid are congruent, the trapezoid is an isosceles trapezoid. The following theorems state the properties of an isosceles trapezoid.

  28. Reading Math Theorem 6-6-5 is a biconditional statement. So it is true both “forward” and “backward.”

  29. Example 3A: Using Properties of Isosceles Trapezoids Find mA. mC + mB = 180° Same-Side Int. s Thm. 100 + mB = 180 Substitute 100 for mC. mB = 80° Subtract 100 from both sides. A  B Isos. trap. s base  mA = mB Def. of  s mA = 80° Substitute 80 for mB

  30. Example 3B: Using Properties of Isosceles Trapezoids KB = 21.9m and MF = 32.7. Find FB. Isos.  trap. s base  KJ = FM Def. of segs. KJ = 32.7 Substitute 32.7 for FM. Seg. Add. Post. KB + BJ = KJ 21.9 + BJ = 32.7 Substitute 21.9 for KB and 32.7 for KJ. BJ = 10.8 Subtract 21.9 from both sides.

  31. Example 3B Continued Same line. KFJ  MJF Isos. trap.  s base  Isos. trap.  legs SAS ∆FKJ  ∆JMF CPCTC BKF  BMJ Vert. s FBK  JBM

  32. Example 3B Continued Isos. trap.  legs  AAS ∆FBK  ∆JBM CPCTC FB = JB Def. of  segs. FB = 10.8 Substitute 10.8 for JB.

  33. In Your Notes Find mF. mF + mE = 180° Same-Side Int. s Thm. E  H Isos. trap. s base  mE = mH Def. of  s mF + 49°= 180° Substitute 49 for mE. mF = 131° Simplify.

  34. In Your Notes JN = 10.6, and NL = 14.8. Find KM. Isos. trap. s base  Def. of segs. KM = JL JL = JN + NL Segment Add Postulate KM = JN + NL Substitute. KM = 10.6 + 14.8 = 25.4 Substitute and simplify.

  35. Example 4A: Applying Conditions for Isosceles Trapezoids Find the value of a so that PQRS is isosceles. Trap. with pair base s  isosc. trap. S  P mS = mP Def. of s Substitute 2a2 – 54 for mS and a2 + 27 for mP. 2a2 – 54 = a2 + 27 Subtract a2 from both sides and add 54 to both sides. a2 = 81 a = 9 or a = –9 Find the square root of both sides.

  36. Example 4B: Applying Conditions for Isosceles Trapezoids AD = 12x – 11, and BC = 9x – 2. Find the value of x so that ABCD is isosceles. Diags.  isosc. trap. Def. of segs. AD = BC Substitute 12x – 11 for AD and 9x – 2 for BC. 12x – 11 = 9x – 2 Subtract 9x from both sides and add 11 to both sides. 3x = 9 x = 3 Divide both sides by 3.

  37. In Your Notes Find the value of x so that PQST is isosceles. Trap. with pair base s  isosc. trap. Q  S mQ = mS Def. of s Substitute 2x2 + 19 for mQ and 4x2 – 13 for mS. 2x2 + 19 = 4x2 – 13 Subtract 2x2 and add 13 to both sides. 32 = 2x2 Divide by 2 and simplify. x = 4 or x = –4

  38. The midsegment of a trapezoidis the segment whose endpoints are the midpoints of the legs. In Lesson 5-1, you studied the Triangle Midsegment Theorem. The Trapezoid Midsegment Theorem is similar to it.

  39. Example 5: Finding Lengths Using Midsegments Find EF. Trap. Midsegment Thm. Substitute the given values. Solve. EF = 10.75

  40. 1 16.5 = (25 + EH) 2 In Your Notes Find EH. Trap. Midsegment Thm. Substitute the given values. Simplify. Multiply both sides by 2. 33= 25 + EH Subtract 25 from both sides. 13= EH

More Related