Download
1 / 10
100 likes | 224 Vues
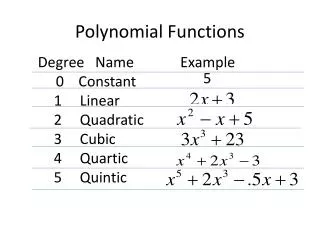
This guide covers the standard form of polynomial functions, detailing how to arrange terms by descending degree. It includes examples for writing polynomials in standard form, classifying them by degree and number of terms, and analyzing their end behavior. Learn about turning points, the transitions between increasing and decreasing intervals, and the maximum number of turning points based on the polynomial's degree. There are also methods to determine the degree of a polynomial using sets of ordered pairs.
E N D
5.1 Polynomial Functions P280-284
Standard form of a polynomial function: Terms are arranged by degree in descending numerical order.
Ex) Write in standard form. Then classify by degree and number of terms. a) b)
Turning point : change in the direction in terms of y…from increasing to decreasing or from decreasing to increasing. Maximum # turning points : n-1, where n is the degree
Ex) Describe the shape of the graph, Including end behavior, turning points, and increasing/decreasing intervals. a)
Ex) Describe the shape of the graph, Including end behavior, turning points, and increasing/decreasing intervals. b)
Given a set of ordered pairs, with consecutive x-values that differ by a constant value, the degree of the polynomial can be determined by looking at when the differences of consecutive y-values become constant.
