IV. Fields

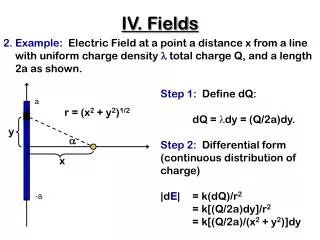
1. IV. Fields 2. Example: Electric Field at a point a distance x from a line with uniform charge density l total charge Q, and a length 2a as shown. Step 1: Define dQ: dQ = ldy = (Q/2a)dy. Step 2: Differential form (continuous distribution of charge) |dE| = k(dQ)/r2 = k[(Q/2a)dy]/r2 = k[(Q/2a)/(x2 + y2)]dy a r = (x2 + y2)1/2 y a x -a

2. IV. Fields 2. Example: Electric Field at a point a distance x from a line with uniform charge density l total charge Q, and a length 2a as shown. Step 3: Identify any symmetry In this case, there is only a net Electric field in the x direction. Why? Ex = {k[(Q/2a)/(x2 + y2)]dy}cos(a) ={k[(Q/2a)/(x2 + y2)]dy}(x/r) ={k[(Q/2a)x/(x2 + y2)3/2]}dy a r = (x2 + y2)1/2 y a x -a

3. IV. Fields 2. Example: Electric Field at a point a distance x from a line with uniform charge density l total charge Q, and a length 2a as shown. Step 4: Integrate a r = (x2 + y2)1/2 y a x -a

4. IV. Fields 2. Example: Electric Field at a point a distance x from a line with uniform charge density l total charge Q, and a length 2a as shown. Step 5: Limiting behavior? a => ∞ a r = (x2 + y2)1/2 y a x -a (IV.A.1)

5. IV. Fields 3. Other cases of interest: P z E = s/2e0 (IV.A.2) (IV.A.2) s infinite plane

6. V. Gauss’s Law. C. Examples • Field of an infinite line charge. a. Step 1: Create a “Gaussian Surface” that exploits the symmetry of the problem. Aim to reduce the integral into an easy product. Note: even before solving the problem previously, we know that the electric field only points radially from the the wire. Why?

7. V. Gauss’s Law. C. Examples • Field of an infinite line charge. b. Step 2: Calculate flux through surfaces. Flux through top and bottom of cylinder: L 0 x

8. V. Gauss’s Law. C. Examples • Field of an infinite line charge. • Step 2: Calculate fluxes • (Step 3: Don’t forget vector direction!) Flux side of Gaussian Cylinder: FE = ∫SE•dA = (E)(2pxL) = Qenc/e0. But l = Qenc/L, so E = (2kl/x), directed in +x-direction. x

9. V. Gauss’s Law. C. Examples 2. Field of an infinite uniformly charged plane. a. Step 1: Create a “Gaussian Surface” that exploits the symmetry of the problem. Aim to reduce the integral into an easy product. x

10. V. Gauss’s Law. C. Examples 2. Field of an infinite uniformly charged plane. a. Step 1: Create a “Gaussian Surface” that exploits the symmetry of the problem. Aim to reduce the integral into an easy product. Flux through sides: 0 Flux through top & bottom: r FE = ∫SE•dA = (E)(2pr2) = Qenc/e0. But s = Qenc/pr2, so E = (s/2e0), directed in the +x- direction x x

11. V. Gauss’s Law. C. Examples 3. Field of a spherical shell of uniform charge a. Step 1: Create a “Gaussian Surface” that exploits the symmetry of the problem. Aim to reduce the integral into an easy product. Inside: no charge enclosed. Outside: total charge Q enclosed.

12. V. Gauss’s Law. C. Examples 3. Field of a spherical shell of uniform charge a. Step 1: Create a “Gaussian Surface” that exploits the symmetry of the problem. Aim to reduce the integral into an easy product. Inside: no charge enclosed. Outside: total charge Q enclosed.