1 / 24

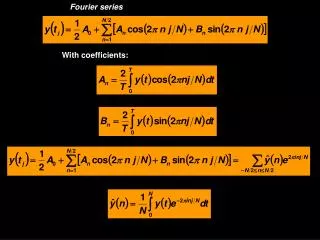
Fourier Series

Fourier Series. Engineering Mathematics – I Prepared By G.VANMATHI, M.Sc.,M.Phil., Assistant Professor / Mat hematics. Content. Periodic Functions Fourier Series. Fourier Series. Periodic Functions. The Mathematic Formulation.

brantr
Télécharger la présentation

Fourier Series

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Fourier Series Engineering Mathematics – I Prepared By G.VANMATHI, M.Sc.,M.Phil., Assistant Professor / Mathematics

  2. Content • Periodic Functions • Fourier Series

  3. Fourier Series Periodic Functions

  4. The Mathematic Formulation • Any function that satisfies where T is a constant and is called the period of the function.

  5. Example: Find its period. Fact: smallest T

  6. Example: Find its period. must be a rational number

  7. Example: Is this function a periodic one? not a rational number

  8. Fourier Series Fourier Series

  9. A periodic sequence f(t) t T 2T 3T Introduction • Decompose a periodic input signal into primitive periodic components.

  10. Synthesis T is a period of all the above signals Even Part Odd Part DC Part Let 0=2/T.

  11. Orthogonal Functions • Call a set of functions {k}orthogonal on an interval a < t < b if it satisfies

  12. Orthogonal set of Sinusoidal Functions Define 0=2/T. We now prove this one

  13. Proof m  n 0 0

  14. Proof m = n 0

  15. Define 0=2/T. Orthogonal set of Sinusoidal Functions an orthogonal set.

  16. Decomposition

  17. Proof Use the following facts:

  18. f(t) 1 -6 -5 -4 -3 -2 -  2 3 4 5 Example (Square Wave)

  19. f(t) 1 -6 -5 -4 -3 -2 -  2 3 4 5 Example (Square Wave)

  20. f(t) 1 -6 -5 -4 -3 -2 -  2 3 4 5 Example (Square Wave)

  21. Harmonics T is a period of all the above signals Even Part Odd Part DC Part

  22. Define , called the fundamental angular frequency. Define , called the n-th harmonicof the periodic function. Harmonics

  23. Harmonics

  24. harmonic amplitude phase angle Amplitudes and Phase Angles

More Related