1 / 6

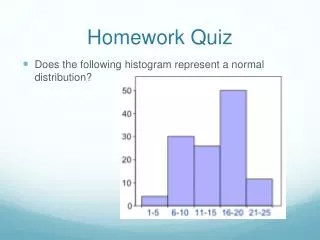
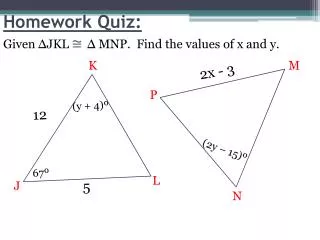
Homework Quiz

This article explains the Rule of 72, a simple formula to estimate how long it takes for an investment to double based on a fixed annual rate of return. For example, at an 8% interest rate, money will double in approximately 9 years. We also analyze Sally's savings for college, starting with $200 at 1% interest compounded annually. The calculations show her savings will grow to $202.04 in three years and to $328.93 after 50 years. If compounded monthly, it increases to $329.68, demonstrating the impact of compounding frequency on savings growth.

china
Télécharger la présentation

Homework Quiz

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Homework Quiz

  2. Rule of 72 Interest Rate Years for money to double 9 years 6 12 36 2400 years • 8% • 12% • 6% • 2% • .03%

  3. I = P x R x T • Sally is saving money for college and she currently has $200 in her savings account. Her bank pays a rate of 1% on her money. If her money compounds annually, what will her account be worth in three years? • I= ??? • P= 200 • R= .01 • T= 1 year (three times)

  4. Solution • 200 x .01 x 1 = 2.00 • 202 x .01 x 1 = 2.02 • 204.02 x .01 x 1 = 2.04 • 206.06

  5. What would she have after 50 years? • 328.93

  6. What if her money compounded monthly? • For fifty years? • 329.68

More Related