1 / 18

Performance Issues in Non-Gaussian Filtering Problems

This study investigates various filtering techniques for tackling non-Gaussian processes in estimation problems. We evaluate the performance of several filters, including the Extended Kalman Filter (EKF), Multiple Model Filter (MMF), Particle Filter (PF), and Point Mass Filter (PMF). By analyzing mean square error (MSE) and Kullback divergence, we reveal important insights about their effectiveness, particularly in handling non-Gaussian posterior distributions. Our findings demonstrate significant differences in performance depending on the method, emphasizing the value of Kullback divergence as a complement to traditional measures.

dacia
Télécharger la présentation

Performance Issues in Non-Gaussian Filtering Problems

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Performance Issues in Non-Gaussian Filtering Problems G. Hendeby, LiU, Sweden R. Karlsson, LiU, Sweden F. Gustafsson, LiU, Sweden N. Gordon, DSTO, Australia

  2. Motivating Problem – Example I • Linear system: • non-Gaussian process noise • Gaussian measurement noise • Posterior distribution:distinctly non-Gaussian

  3. Motivating Problem – Example II • Estimate target position based on two range measurements • Nonlinear measurements but Gaussian noise • Posterior distribution: bimodal

  4. Filters The following filters have been evaluated and compared • Local approximation: • Extended Kalman Filter (EKF) • Multiple Model Filter (MMF) • Global approximation: • Particle Filter (PF) • Point Mass Filter (PMF, representing truth)

  5. Filters: EKF EKF: Linearize the model around the best estimate and apply the Kalman filter (KF) to the resulting system.

  6. Filter 1 Filter 1 Filter 1 Filter 1 Mix Filter 2 Filter 2 Filter M Filter M Filters: MMF • Run several EKF in parallel, and combine the results based on measurements and switching probabilities

  7. Filters: PF Simulate several possible states and compare to the measurements obtained.

  8. Filters: PMF • Grid the state space and propagate the probabilities according to the Bayesian relations

  9. Filter Evaluation (1/2) Mean square error (MSE) • Standard performance measure • Approximates the estimate covariance • Bounded by the Cramér-Rao Lower Bound (CRLB) • Ignores higher-order moments!

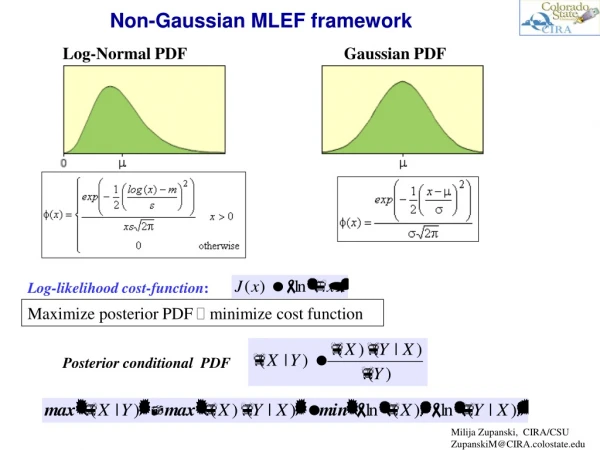
  10. Filter Evaluation (2/2) Kullback divergence • Compares the distance between two distributions • Captures all moments of the distributions

  11. Filter Evaluation (2/2) Kullback divergence – Gaussian example • Let • The result depends on the normalized difference in mean and the relative difference in variance

  12. Example I • Linear system: • non-Gaussian process noise • Gaussian measurement noise • Posterior distribution:distinctly non-Gaussian

  13. Simulation results – Example I • MSE similar for both KF and PF! • KL is better for PF, which is accounted for by multimodal target distribution which is closer to the truth

  14. Example II • Estimate target position based on two range measurements • Nonlinear measurements but Gaussian noise • Posterior distribution: bimodal

  15. Simulation results – Example II (1/2) • MSE differs only slightly for EKF and PF • KD differs more, again since PF handles the non-Gaussian posterior distribution better

  16. Simulation results – Example II (2/2) • Using the estimated position to determine the likelihood to be in the indicated region • The EKF based estimate differs substantially from the truth

  17. Conclusions • MSE and Kullback divergence evaluated as performance measures • Important information is missed by the MSE, as shown in two examples • The Kullback divergence can be used as a complement to traditional MSE evaluation

  18. Thanksforlistening Questions?

More Related