1 / 13

Introduction to Logarithms

This lesson provides a comprehensive overview of logarithms, focusing on exponential growth and decay. It introduces key concepts such as initial value (y-intercept) and growth/decay rates. We explore a practical example involving a bacteria population that doubles every hour, starting from an initial sample of 40. The lesson poses questions about calculating population after a certain duration and determining the time needed to reach a specific population. Additionally, we cover finding the inverse of exponential functions and their application in real-world scenarios.

damara
Télécharger la présentation

Introduction to Logarithms

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

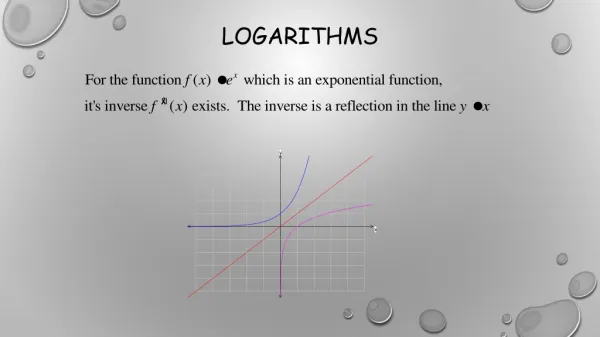
  1. Introduction to Logarithms Lesson 7.3

  2. Review: y = abx • a: initial value/y-intercept • b: growth rate • Growth: b > 1 • Decay: 0 < b < 1

  3. A bacteria population doubles every hour. If you start with a sample of 40 bacteria, how many will there be in 3 hours?

  4. A bacteria population doubles every hour. If you start with a sample of 40 bacteria, after how many hours will there be 1000 bacteria present?

  5. a power m n b

  6. 2 0 4 4 2 0

  7. -3 -1 -2 -2 -1 -3

  8. 2 .903 .602 1.857

  9. 2.079 1 1.099 1 0 -.288

  10. Find the inverse:

More Related