Vectors MM1 module 4

1. VectorsMM1 module 4 Poul Nielsen

2. Vectors module 4 objectives • After this module you should have a clear understanding of: • Coordinate systems; • The properties of vectors; • Vector length, scalar multiplication, addition, and subtraction; • The dot product and its properties; • Resolving vector components; • The cross product and its properties; • How to find equations of lines; • How to find equations of planes.

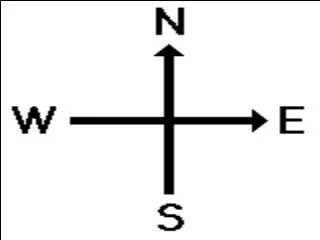
3. Coordinate systems • A coordinate system is a system for specifying points in n–dimensional space using coordinates. • A coordinate is a set of n variables which fix a geometric object. • The simplest coordinate system consists of n coordinate axes oriented perpendicularly to each other, known as Cartesian coordinates (René Descartes 1637). • In this module we will focus our attention on 2–dimensional and 3–dimensional Cartesian coordinate systems.

4. Right handed coordinate systems are usually chosen by convention. Left handed coordinate systems are occasionally encountered. Coordinate systems in 3D

5. Coordinate planes in 3D • The 3–dimensional Cartesian coordinate system defines 3 natural coordinate planes by taking coordinate axes in pairs. • Illustrated below are the xy–, yz–, and zx–coordinate planes, respectively.

6. Points in 3D • A point in a 3–dimensional coordinate system can be characterised by a set of 3 real numbers, representing the distances along the x–, y–, and z–coordinate axes. • e.g. the point p at x = 4, y = –6, and z = 5.Note: the order of movement is not important

7. Coordinate systems in 2D • In 2 dimensions right handed coordinate systems are usually chosen by convention(constructed like a 3–dimensional coordinate system with the z–coordinate axis pointing towards the viewer). • A point in a 2–dimensional coordinate system can be characterised by a set of 2 real numbers, representing thedistances along thex– and y–coordinate axes. • e.g. the point p atx = 4, y = –6

8. Vector • A vector is essentially a directed arrow. • A vector has the properties of length and direction, but not position. • Two vectors are equal if they have the same length and the same direction. • A vector from point p to point q has its tail at p and its head at q. • A vector with its tail at the coordinate origin is sometimes called a position vector.

9. What are vectors used for? • Computer graphics; • CAD/CAM; • Characterisation of force and/or flow fields in analysis of solid and fluid systems; • Representation of state variables to describe complex systems.

10. Vector component notation • Vectors can be described in component notation as n 1 matrices where the elements represent the components of the vector along each coordinate axis. • The number of components is its dimension. • e.g. the 2–dimensional vector, v, illustrated below has components 4 and 3 units along the x– and y–axes, respectively.It can be represented incomponent notation as

11. Specifying vectors and components • Vectors are generally denoted by lowercase, non-italicised, bold characterse.g. u, v, w will be commonly used. • Components of vectors are usually denoted by lowercase, italicised, non-bold characters with an index as a subscripte.g. u3 refers to the 3rd component of vector u. • More generally, an n–dimensional vector, v, can be written as

12. Length of a vector • The length of a vector v, denoted |v|, can be readily calculated from its components, vi • if • then • e.g. for

13. Zero vector • A zero vector, denoted 0, is a vector of length zero. • All the components of a zero vector are zero. • The zero vector is the additive identityi.e. v + 0 = v • Listed below are zero vectors for 1–, 2–, 3–, and n–dimensions

14. Unit vector • A unit vector is a vector of length 1, sometimes called a direction vector. • An arbitrary vector, v, can be converted to a unit vector, , by dividing each of its components by its length • e.g. is a vector of unit length with the same direction as the vector

15. Base vectors… • A coordinate system provides a natural set of base vectors of unit length with direction in each of the coordinate axes. • In a 2–dimensional coordinate system with coordinate axes x and y, the base vectors are denoted and , respectively. • In a 3–dimensional coordinate system with coordinate axes x, y, and z, the base vectors are denoted , , and

16. …Base vectors • Any vector can be expressed in terms of its coordinate base vectors • For an n–dimensional coordinate system with coordinates x1, x2, … xn, and base vectors

17. Vector scalar multiplication • Multiplying an n–dimensional vector by a scalar results in an n–dimensional vector with each of its elements multiplied by the scalar. • e.g. • Note: the length scales by c but the direction remains the same (or is reversed if c < 0).

18. Vector negation • Multiplying an n–dimensional vector by –1 results in a vector of the same length but reversed direction.

19. Vector addition… • Vector addition is the operation of adding two or more vectors together into a vector sum. • For vectors u and v, the vector sum u + v is obtained by placing them head to tail and drawing the vector from the free tail to the free head. • Note that u + v = v + u • Vectors being added must have the same dimension

20. …Vector addition • In Cartesian coordinates, vector addition can be performed simply by adding the corresponding components of the vectors • e.g.

21. Vector subtraction… • A vector difference is the result of subtracting one vector from another. • A vector difference is denoted using the normal minus sign, i.e., the vector difference of vectors u and v is written u – v. • A vector difference is equivalent to a vector sum with the orientation of the second vector reversed, i.e. u – v = v + (–u)

22. …Vector subtraction • In Cartesian coordinates, vector subtraction can be performed simply by subtracting the corresponding components of the vectors • e.g.

23. Vector between two points • If p and q are two points with position vectors p and q, respectively, then the vector joining p to q is q – p. • The finite line segment starting at p and terminating at q is denoted • Remember as final – initial.

24. Dot product… • The dot product can be defined for two n–dimensional vectors u and v byu•v = |u| |v| cos() where  is the angle between the vectors and |u| and |v| are the lengths of u and v, respectively. • Note that the dot product of two vectors results in a scalar.

25. …Dot product… • In Cartesian coordinates, the dot product can be performed by summing the products of the corresponding components of the vectors • e.g.

26. …Dot product • The dot product, u•v, has the geometric interpretation as the length of v times the length of the projection of u onto v when the two vectors are placed so that their tails coincide.

27. Dot product properties • The dot product is commutative, u•v = v•u.This follows from the definitions:u•v = |u| |v| cos() = |v| |u| cos() = v•uu•v = u1v1 + u2v2 + …unvn = v•u • The dot product is distributive, u•(v + w)= u•v + u•w • The associative property, (u•v)•w = v•(u•w), is meaningless as (u•v)•w is not defined since (u•v) is a scalar and cannot be dot multiplied. • From u•u = u12 +  u22 + …un2 and it follows that |u|2 = u•u

28. Perpendicular vectors… • Two vectors are perpendicular if the angle between them is a right angle(i.e. /2 radians or 90°). • Since u•v = |u| |v| cos() and cos(/2) = 0, it follows that two non–zero vectors u and v are perpendicular if, and only if, u•v = 0. • e.g.So u and v are perpendicular.

29. Dot product of base vectors • Recall that in a Cartesian coordinate system the base vectors are mutually perpendicular and of unit length. • Thus in 2–dimensions:in 3–dimensions:in n–dimensions:

30. Finding angles between vectors… • Since u•v = |u| |v| cos() and u•v = u1v1 + u2v2 + …unvnthe dot product can be used to find the angle, , between vectors u and v • e.g.

31. …Finding angles between vectors • e.g.

32. Projection of vector on vector… • Given a vector u, find its projection p in the direction of vector v.

33. …Projection of vector on vector • e.g. find the projection of u on v, where

34. Resolving vector components… • The projection formula can be used to resolve a vector, u, parallel, u||, and perpendicular, u, to a direction, v. • e.g. resolve u into vectorsparallel and perpendicular to v, where

35. …Resolving vector components • e.g. resolve the vector, u, parallel, u||, and perpendicular, u, to the vector, v, where

36. Cross product… • For 3–dimensional vectors u and v, the cross product is defined asuv = |u| |v| sin() where  is the angle between the vectors, |u| and |v| are the lengths of u and v, and is the unit vector normal to the plane containing u and v. • The cross product uses theright hand rule to determinethe direction of the result.i.e. u, v, and uv form aright handed system.

37. …Cross product • Ensure that you understand how to orient uv relative to u and v using the right hand rule.

38. Cross product properties • The cross product is anti–commutative, uv = –vu.This is a consequence of the right hand rule. • The cross product is distributive, u(v + w)= uv + uw • For a scalar c, (cu)v = c(uv) • Note that the cross product operates on two 3–dimensional vectors to produce a 3–dimensional vector perpendicular to the first two. • Question: What do you get when you cross a mountain-climber with a mosquito?Answer: Nothing: you can't cross a scaler with a vector.

39. Aside: determinant of 33 matrix… • Determinants are very useful in the analysis and solution of systems of linear equations. A nonhomogeneous system of linear equations has a unique solution iff the determinant of the system's matrix is nonzero (i.e., the matrix is nonsingular) • Recall that if A is a 2  2 matrix, then the determinant of A is denoted by det(A) = |A| = a11a22 – a21a12 • e.g.

40. …Aside: determinant of 33 matrix… • If A is a 3  3 matrix, then the determinant of A may be calculated using the formula

41. …Aside: determinant of 33 matrix… • Remember using the following pattern

42. …Aside: determinant of 33 matrix… • e.g.

43. …Aside: determinant of 33 matrix • e.g.

44. Cross product calculation… • In Cartesian coordinates, the cross product can be calculated using the following method

45. …Cross product calculation… • Remember using the following pattern

46. …Cross product calculation… • e.g.

47. …Cross product calculation • e.g.

48. Area of a parallelogram • If a parallelogram is defined by the vectors u and v then the area of the parallelogram is given by |uv| • i.e.

49. Lines • A line is a straight one-dimensional figure having no thickness and extending infinitely in both directions. A line is sometimes called a straight line. • A line is uniquely determined by either: • two points; or • a point and a direction vector.

50. Line defined by two points… • The line passing through points p and q is denoted • Recall that if p and q are two points with position vectors p and q, respectively, then the vector joining p to q is q – p. • We can thus define the line that passes through points p and q parametrically as x = p + (q – p)twhere t is a parameter that defines the position on the line (i.e. x = p at t = 0, and x = q at t = 1).