1 / 27

Understanding Percents: Homework Warm-Up and Real-Life Applications

Join us on Tuesday, December 6th, for a warm-up session on finding percents! Confirm if you've done your homework and get ready to practice writing fractions and decimals as percentages. We'll explore the concept of percent proportion, solve for the part, and find the whole from given percentages. Enhancing your understanding through exercises, you'll see how to apply these math skills in real-life scenarios, like school fundraising programs. Don’t forget to enjoy a corny joke while learning!

dong
Télécharger la présentation

Understanding Percents: Homework Warm-Up and Real-Life Applications

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

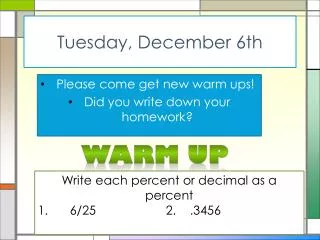
  1. Tuesday, December 6th Please come get new warm ups! Did you write down your homework? Warm Up Write each percent or decimal as a percent 1. 6/25 2. .3456

  2. Corny Joke of the Day What do you call a cow who can’t give milk? An “udder” failure!

  3. Do you Remember? • When you make a decimal a percent you can really move the decimal _______ places to the ___________. • When you make a fraction a percent you want to make an equivalent fraction that has a denominator of _____________________.

  4. Homework Answers

  5. Finding Percents Of a Number

  6. The Meat of it • A percent proportion compares part of a quantity to the whole quantity, this is called the base. • The percent is always written as a fraction with a denominator of 100. “Per” means out of, and “cent” refers to 100. • Ratio Part (is) and whole (of)

  7. Setting it up

  8. Three ways you will see a problem Fill in your table!!!

  9. Caution You will have to solve proportions to work with percents!

  10. Proportion Review Cross Multiply and Divide

  11. Part 1 Finding the percent

  12. What percent of 6 is 3? 100 ÷ 2=50

  13. You Try #1 What percent of 5 is 2?

  14. You Try #2 What percent of 12 is 7?

  15. Part 2 Finding the Part

  16. What number is 50% of 6 6 ÷ 2=3

  17. You Try #1 What number is 25% of 24

  18. You Try #2 What number is 10% of 32

  19. Part 3 Finding the Whole

  20. What number is 3 is 50% of what number? 6 ÷ 1=6

  21. You Try #1 What number is 11 25% of?

  22. You Try #2 What number is 15 30% of

  23. Real Life Application

  24. There are 480 students in Sara’s school. If 70% of the students participate in the fundraising program, how many students participate in the fundraising program?

  25. s 70 33,600 100s ___ ___ _____ ____ 100 100 100 480 Answer Now solve: Let s represent the number of students who participate in the fundraising program. = The cross products are equal. 100 •s = 70 • 480 100s= 33,600 s is multiplied by 100. Divide both sides of the equation by 100 to undo multiplication. = s = 336 Since 336 is close to your estimate of 375, 336 is a reasonable answer. 336 students participate in the fundraising program.

  26. Tanner is 25% of the way through his exercises. If he has exercised for 20 minutes so far, how much longer does he have to work out?

  27. is % 25 20 __ ___ ___ __ m 100 100 of Answer 25% of the exercises are completed, so 20 minutes is 25% of the total time needed. = Set up a proportion. The “of” part is what you have been asked to find. = The cross products are equal. 100 • 20= 25 •m

More Related