Functional Decompositions for Hardware Verification
390 likes | 599 Vues
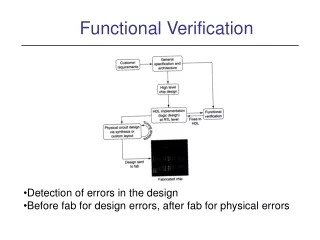
Functional Decompositions for Hardware Verification. With a few speculations on formal methods for embedded systems Ken McMillan. Verification approaches. Informal verification (testing) risk of “escapes” Partial formal verification prove, for example, no arithmetic overflow

Functional Decompositions for Hardware Verification
E N D
Presentation Transcript
Functional Decompositionsfor Hardware Verification With a few speculations on formal methods for embedded systems Ken McMillan
Verification approaches • Informal verification (testing) • risk of “escapes” • Partial formal verification • prove, for example, no arithmetic overflow • can use very coarse abstractions • Formal functional verification • verify against functional spec
Outline • Formal functional verification for hardware • combined theorem proving/ model checking • proof decomposition strategies that allow coarse abstractions • Prospects of application to embedded systems • how are embedded systems different p.o.v. formal verification? • how might we apply formal hardware verification methods to embedded systems?
Mixed approach • Model checking • automated verification of finite state systems • limited in scale by “state explosion problem” • Theorem provers • in principle can “scale up” • in practice require substantial manual guidance • Mixed approach • use theorem prover to break large problems into small, model-checkable problems
Proof decomposition: • reduction to decidable/tractable problems • do it in as few (and as simple) steps as possible Undecidable/ intractable Proof goal proof assistant Decidable/ tractable sub sub sub sub ...but how?
Structural decompositions • intermediate assertions must be temporal • q captures everything M2 must know about M1 • intermediate assertions can be quite complex {p} M1 {q} {q} M2 {r} {p} M1||M2 {r}
Functional decompositions • Divide by “units of work” and not by syntax • instructions • packets • etc. • Much simpler intermediate assertions • interaction between “units of work” is simpler than between system components • Abstraction to finite state • if each “unit of work” uses finite resources • temporal assertions become model-checkable
Example : packet router input buffers output buffers • Unit of work is a packet • Packets don’t interact • Each packet uses finite resources • specializing the property allows a much coarser abstraction Switch fabric
Refinement framework • Refinement relations • Specify intermediate results with respect to reference model • Each intermediate result uses finite • operations • storage locations • Thus, can reduce local verification problems to finite state • Use circular proof! Reference model refinement relations System
“Circular” proofs Reference model f1 up to t -1 implies f2 up to t f2 up to t -1 implies f1 up to t always f1 and f2 or, in temporal logic... Ø(f2 U f1) Ø(f1 U f2) G(f1Ùf2) O.K., but how do we break into “units of work”?
Temporal case splitting p1 p2 p3 p4 p5 ... v1 f: I'm O.K. at time t. Idea: parameterize on most recent writer w at time t. "i: piÞ G((w=i) Þf) (Ùi pi) Þ Gf Rule can be used to decompose large arrays
Combine with “circular” reasoning p1 p2 p3 p4 p5 ... v1 f: I'm O.K. at time t. To prove case w=i at time t, assume general case up to t-1: "i: piÞf®1 ((w=i) Þf) (Ùi pi) Þ Gf still have unbounded cases to prove...
Freeing processes ... p1 p2 p3 p4 p5 v1 f: I'm O.K. at time t. "i: piÞf®1 ((w=i) Þf) (Ùi pi) Þ Gf
Abstract interpretation • Problem: variables range over unbounded set U • Solution: reduce U to finite set Û by a parameterized abstraction, e.g., where U\i represents all the values in U except i. • Need a sound abstract interpretation, s.t.: if f is valid in the abstraction, then, for all parameter valuations, f is valid in the original. Û = {{i}, U\i}
Data type abstractions in SMV • Abstract values represent sets of concrete values • For sound abstraction of operator f, we need: • Examples: • Equality Û = {{i}, U\i} f(ax) £a(fx) = {i} U\i {i} 1 0 U\i 0 ^
Abstraction, continued... • Arrays and function symbols • Other operators ... • boolean operators • temporal operators • quantifiers • arithmetic/inequalities x {i} U\i f(x) f(i) ^ Unbounded array reduced to one fixed element!
OP,DST OP,DST OP,DST opra opra opra oprb oprb oprb Illustration: Tomasulo’s algorithm • Execute instructions in data flow order VAL/TAG REG FILE VAL/TAG TAGGED RESULTS VAL/TAG VAL/TAG EU INSTRUCTIONS OPS EU EU
OP,DST OP,DST opra opra oprb oprb Functional decomposition • “Unit of work” is the instruction VAL/TAG REG FILE VAL/TAG TAGGED RESULTS VAL/TAG VAL/TAG EU EU INSTRUCTIONS OPS EU EU OP,DST opra oprb
OP,DST OP,DST opra opra oprb oprb Functional decomposition • Break instruction into operand fetch and op VAL/TAG REG FILE VAL/TAG TAGGED RESULTS VAL/TAG VAL/TAG EU INSTRUCTIONS OPS EU EU OP,DST opra oprb
OP,DST opra oprb Intermediate assertion • All previous instructions produce correct res VAL/TAG REG FILE VAL/TAG TAGGED RESULTS VAL/TAG VAL/TAG OP,DST EU opra oprb INSTRUCTIONS OPS EU EU OP,DST opra oprb
Points about this proof • Three simple intermediate assertions • operands of instruction are correct • results of instruction are correct • one non-interference property • No invariants about control state • No syntactic decomposition • Abstract interpretation reduces model to finite • Much simpler than proof by invariant is there a useful structural decomposition?
VAL/TAG REG FILE VAL/TAG RETIRED RESULTS VAL/TAG VAL/TAG BUF d e c EU PM INSTRUCTIONS OPS EU RES BUF EU BUF PC branch results OP,DST OP,DST OP,DST opra oprb opra opra oprb oprb branch predictor DM LSQ A more complex example • Unit of work = instruction pc
Scaling problem • Must consider up to three instructions: • instruction we want to verify • up to two previous instructions • Soln: break instruction up into parts • write intermediate assertions ==> too much state for model checker
VAL/TAG REG FILE VAL/TAG RETIRED RESULTS VAL/TAG VAL/TAG BUF d e c EU PM INSTRUCTIONS OPS EU RES BUF EU BUF PC branch results OP,DST OP,DST OP,DST opra oprb opra opra oprb oprb branch predictor DM LSQ Memory operation • Abstract out unneeded components specify LSQ data
Points about this proof • No interface specifications • specify internal data structures of units • No invariants on control state • First decomposition is function al • then abstract out structural components • Compared to similar proof using invariants... • invariant proof approx. 2MB (!) • this proof approx. 20 KB
FLASH cache protocol • Distributed protocol • Maintains consistency of N processor caches P C P C P C P C P C home dir mem • Reference model is “programmer’s model” of memory • Unit of work = read/write
Proof decomposition P C writer • Unit of work = read/write • Non-interference lemmas • No two exclusive copies in network • No unexpected invalidate acks fwd interference Abstracted nodes ack put P C home P C get reader
p1(t1) p2(t2) p3(t3) p4(t4) Lamport's Bakery algorithm ... non-critical section read all tickets choose one larger wait for all processes with smaller ticket critical section
pj(tj) pi(ti) Liveness proof (Qadeer and Saxe) • Unit of work = ticket number • Split cases on process pj that process pi is waiting for... • Assume by induction that j terminates if tj<ti. • Note, pj must get higher ticket than pi on next iteration* • By induction on j, process pi exits wait loop ... ... ... • Note: • reduction to finite number of processes • model checking gets property * automatically
Points about this proof • No invariants used • Two liveness lemmas: • one for termination of each loop • these reference specific code lines, but... • No syntactic decomposition used
Overview of approach • Specify by temporal refinement relations • “circular” temporal argument • Specialize properties by restricting to a single “unit of work” • temporal “case splitting” • Abstract to finite-state • specialization allows a coarser abstract interpretation This approach is supported by a special purpose proof assistant, built on the SMV model checker
Application to embedded systems • Generic software issues • Issues specific to embedded systems
Why is HW easier than SW? • Finite-state is not the issue • Proofs above did not depend on bounded state • “Bad” aspects of software • global store (hardware term: bottleneck) • any component can “interfere” with any other • we can expect an explosion of non-interference lemmas • pointers are a chief culprit • inductive data structures • requires complex invariants for recursive functions • arithmetic? • real time?
Can we make SW more HW-like? • More structured communication • allows coarser abstractions for verification without introducing interference • good examples: Esterel, Polis, etc. • Increase grain of atomicity • analog of clock cycle • Separate timing from functionality • as in synchronous hardware Trends are in these directions, although languages are problematic (esp. C++)
Embedded systems issues • How do embedded systems differ from other systems, from an FV point of view? • hardware differences • processors tend to be simpler (good) • many and heterogeneous processors • hard real time (see above) • greater software/hardware interaction • more precisely: interaction at less abstract level
Abstracting hardware arch. • Use FV to construct abstract reference models of custom hardware software model HW reference model refinement relation hardware implementation
Abstracting HW/SW comps • Next layer up is provided by driver software driver reference model refinement relation software driver HW reference model
“Platform” based design • Build an abstract layer using synthesis tools • Formal framework for integrating models constraint syntax compilation/ synthesis refinement relations syntax intf
Conclusions • Functional approach to proof decomposition • divide problem into “units of work” • allows coarse abstractions for model checking • proof effort appears to scale well with system size • supported by special-purpose proof assistant • Issues for application to embedded systems • Needs more structured communication • Needs separation of timing and function • Can provide reference models to abstract hardware/software interface • Can support platform-based design