1 / 16

Projectile Motion

This document provides a comprehensive overview of projectile motion, detailing how objects move under the influence of gravity after an initial thrust. Key concepts include the independence of vertical and horizontal motion, and the formulas to calculate distance, velocity, and time for projectiles. Through examples such as a stone thrown from a cliff and a ball launched horizontally, it illustrates the fundamental principles of projectile motion. Learn how to apply these concepts to determine flight time, horizontal distance, and vertical speed upon impact.

frye
Télécharger la présentation

Projectile Motion

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

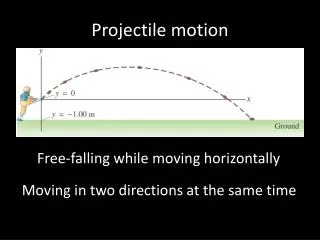
  1. Projectile Motion

  2. Projectile • An object that moves through the air only under the influence of gravity after an initial thrust • For simplicity, we’ll use 9.8 m/s2 for gravity. • Trajectory – path of a projectile

  3. The vertical and horizontal components of a projectile are independent of each other • If 1 ball were dropped and another ball launched forward from the same height, they would hit the ground at the same time.

  4. Video Break • Mythbusters

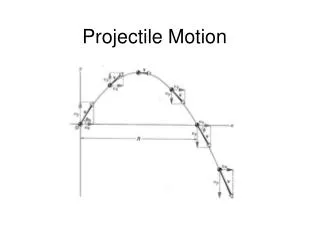
  5. Force vectors for projectiles • Draw both horizontal and vertical vectors

  6. VerticalHorizontal d = Vt V = d/t d = ½ gt2 V = gt

  7. Horizontally launched cannonball

  8. Non-horizontally launched cannonball

  9. Vertical Component • Distance • d = Vit + ½ gt2 *Vi is 0, so it cancels! • d = ½ gt2 • Velocity • Vf = Vi + gt *Vi is 0, so it cancels! • V = gt

  10. Horizontal Component • Distance • d = Vt • Velocity • V = d/t

  11. Example) A stone is thrown horizontally at 15 m/s from the top of a cliff 44 m high. • a) How long does it take to fall? • d = ½ gt2 • 44 = ½ (9.80)(t2) • 44 = 4.90( t2) • 8.9796 = t2 • t = 3.0 s 15m/s 44m

  12. Example) A stone is thrown horizontally at 15 m/s from the top of a cliff 44 m high. • b) How far from the base of the cliff does it land? • d = Vt • d = (15)(3.0) • d = 45 m d

  13. Example) A stone is thrown horizontally at 15 m/s from the top of a cliff 44 m high. • c) What is its vertical speed when it hits the ground? • V = gt • V = (9.80)(3.0) • V = 29.4 m/s

  14. Example 2) A ball is thrown at a horizontal speed of 18 m/s. It’s flight time is 4.6 seconds. • How high does the ball go? • d = ½ gt2 • d = ½ (9.80)(2.32) • d = 25.92 m

  15. Example 2) A ball is thrown at a speed of 18 m/s. It rises and falls in 4.6 seconds. • How far away does it land? • d = Vt • d = (18)(4.6) • d = 82.8 m

  16. Example 2) A ball is thrown at a speed of 18 m/s. It rises and falls in 4.6 seconds. • What is its vertical speed when it hits the ground? • V = gt • V = (9.8)(2.3) • V = 22.54 m/s

More Related