1 / 13

Exploring Trigonometry: Angles and the Law of Sines

In this lesson on trigonometry, we tackle a real-world problem involving a 13-foot ladder against a 12-foot house to find the angle it forms with the ground. We will also solve several problems using the Law of Sines, including determining the lengths of sides and the measures of angles in non-right triangles. Focus on the importance of understanding triangle relationships, especially before the upcoming unit test next Tuesday. Additionally, students with missing quizzes are reminded to make them up today after school.

gabi
Télécharger la présentation

Exploring Trigonometry: Angles and the Law of Sines

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

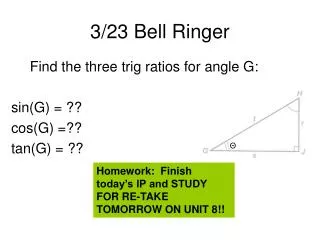
  1. 3/10 Adv. Alg/Trig Bell Ringer 1. A 13-foot ladder rests on a 12-foot tall house. What angle does the ladder form with the ground? 2. Solve: HW Finish Law of Sines Independent Practice

  2. 3/10 News and Notes • Perfection: 4th • Missing Quizzes: Must be made up today after school!!! • Unit Test next Tuesday!

  3. Missing Quizzes due to AP • 2nd: Jazmyn, Jahmeelah, Ronnell, Jesus G, Jasmin H, Maria • 4th: Christian, Carlos, Victor, Jesus TODAY AFTER SCHOOL IN ROOM 218!!! Or by appointment

  4. Solve for b C b 350 cm 59° 38° A B

  5. You Just Got TREATED! TREATED! TREATED!

  6. Quick check • Up to this point, what types of triangles have we been able to use trigonometry with? • RIGHT TRIANGLES!!! • Today’s Goal?! • Apply trigonometry to triangles that are NOT right triangles.

  7. Solve for b C b 350 cm 59° 38° A B Law of Sines:

  8. Solve for b and c C b 350 cm 59° 38° A B c

  9. C b 350 cm • First find angle C 180-59-38 = C 83 = Angle C 38° A B c

  10. Solve for c – Beat the Clicker! C b 350 cm 59° 38° A B c

  11. Does our answer make sense? C • Is the longest side across from largest angle? • Is the shortest side across from shortest angle? 83° 251 cm 350 cm 59° 38° A B 405 cm

  12. Independent Practice • Practice using the Law of Sines! What you don’t finish is for homework. • We’ll finish with an Exit Ticket!

  13. Exit Ticket – Round answer to nearest whole number! B • Solve for w • What’s the measurement of angle B? 28cm w 79° 52° W C HW Finish Law of Sines Independent Practice

More Related